
【题目】已知任意三角形ABC,
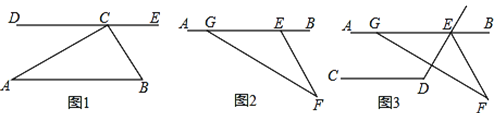
(1)如图1,过点C作DE∥AB,求证:∠DCA=∠A;
(2)如图1,求证:三角形ABC的三个内角(即∠A、∠B、∠ACB)之和等于180°;
(3)如图2,求证:∠AGF=∠AEF+∠F;
(4)如图3,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F.
【答案】(1)证明见解析(2)三角形的内角和为180°(3)∠AGF=∠AEF+∠F(4)29.5
【解析】试题分析:(1)根据平行线的性即可得到结论;
(2)因为平角为180°,若能运用平行线的性质,将三角形三个内角集中到同一顶点,并得到一个平角,问题即可解决;
(3)根据平角的定义和三角形的内角和定理即可得到结论;
(4)根据平行线的性质得到∠DEB=119°,∠AED=61°,由角平分线的性质得到∠DEF=59.5°,根据三角形的外角的性质即可得到结论.
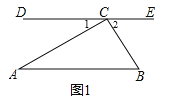
试题解析:证明:(1)∵DE∥BC,∴∠DCA=∠A;
(2)如图1所示,在△ABC中,∵DE∥BC,∴∠B=∠1,∠C=∠2(内错角相等).
∵∠1+∠BAC+∠2=180°,∴∠A+∠B+∠C=180°.
即三角形的内角和为180°;
(3)∵∠AGF+∠FGE=180°,由(2)知,∠GEF+∠EG+∠FGE=180°,∴∠AGF=∠AEF+∠F;
(4)∵AB∥CD,∠CDE=119°,∴∠DEB=119°,∠AED=61°,∵GF交∠DEB的平分线EF于点F,∴∠DEF=59.5°,∴∠AEF=120.5°,∵∠AGF=150°,∵∠AGF=∠AEF+∠F,∴∠F=150°﹣120.5°=29.5°.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】目前甲型H1N1流感病毒在全球已有蔓延趋势,世界卫生组织提出各国要严加防控,因为曾经有一种流感病毒,若一人患了流感,经过两轮传染后共有81人患流感.如果设每轮传染中平均一个人传染x个人,那么可列方程为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:优秀;B:良好;C:合格;D:一般;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:(1)本次调查中,王老师一共调查了多少名同学?
(2)将上面的条形统计图补充完整;并求出“D”所占的圆心角的度数;
(3)从被调查的A类和D类学生中分别选取一位同学进行“一对一”互助学习,请求出所选两位同学恰好是一位男同学和一位女同学的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= ,b= ,且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com