
如图,一个矩形恰好分成六个正方形,其中最小的正方形面积为1cm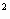 ,求这个矩形的面积.
,求这个矩形的面积.
|
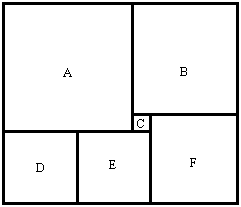
解:设 A、B、C、D、E、F分别表示六个正方形,C的边长为1cm,设正方形A的边长为xcm,则B的边长为(x-1)cm,F的边长为(x-2)cm,D和E的边长均为(x-3)cm.由矩形的对边相等,得方程x+(x-1)=2(x-3)+(x-2).解得x=7.又矩形的一边为 [x+(x-3)]cm,另一边为[x+(x-1)]cm.将x=7分别代入,求得矩形的两边分别为11cm和13cm.所以矩形的面积为11×13=143( ). ). |
|
解这个问题,首先考虑题中有多少个未知量:矩形长、宽、面积,五个正方形的边长及面积.关键在于选择哪一种未知量用 x来表示,其他未知量用x的式子来表示.如果选择矩形的长、宽、面积,五个正方形的面积中的任一个用x的式子来表示都不好,只有选取五个正方形的边长中的一个用x来表示,其他四个正方开的边长用x的式子来表示才适当. |


科目:初中数学 来源: 题型:
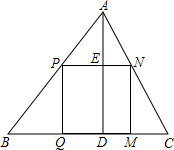 形的一边在BC上,其余两个顶点分别在AB、AC上.设该矩形的长QM=y毫米,宽MN=x毫米.
形的一边在BC上,其余两个顶点分别在AB、AC上.设该矩形的长QM=y毫米,宽MN=x毫米.| 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k | x |

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解


查看答案和解析>>
科目:初中数学 来源: 题型:

 (
( ),当
),当 时,
时, )
)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com