
ЁОЬтФПЁПЮЊСЫДЋГажаЛЊУёзхгХауДЋЭГЮФЛЏЃЌЮвЪаФГжабЇОйааЁАККзжЬ§аДЁББШШќЃЌШќКѓећРэВЮШќбЇЩњЕФГЩМЈЃЌНЋбЇЩњЕФГЩМЈЗжЮЊAЃЌBЃЌCЃЌDЫФИіЕШМЖЃЌВЂНЋНсЙћЛцжЦГЩЭМ1ЕФЬѕаЮЭГМЦЭМКЭЭМ2ЩШаЮЭГМЦЭМЃЌЕЋОљВЛЭъећЃЎЧыФуИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
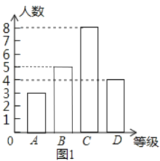
ЃЈ1ЃЉЧѓВЮМгБШШќЕФбЇЩњЙВгаЖрЩйУћЃПВЂВЙШЋЭМ1ЕФЬѕаЮЭГМЦЭМЃЎ
ЃЈ2ЃЉдкЭМ2ЩШаЮЭГМЦЭМжаЃЌmЕФжЕЮЊ_____ЃЌБэЪОЁАDЕШМЖЁБЕФЩШаЮЕФдВаФНЧЮЊ_____ЖШЃЛ
ЃЈ3ЃЉзщЮЏЛсОіЖЈДгБОДЮБШШќЛёЕУAЕШМЖЕФбЇЩњжаЃЌбЁГі2УћШЅВЮМгШЋЪажабЇЩњЁАККзжЬ§аДЁБДѓШќЃЎвбжЊAЕШМЖбЇЩњжаФаЩњга1УћЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЗЈЧѓГіЫљбЁ2УћбЇЩњЧЁКУЪЧвЛУћФаЩњКЭвЛУћХЎЩњЕФИХТЪЃЎ

ЁОД№АИЁПЃЈ1ЃЉВЮШќбЇЩњЙВ20ШЫЃЛВЙЭММћНтЮіЃЛЃЈ2ЃЉ40ЃЛ72ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЁАAЕШМЖЕФШЫЪ§ЁТAЕШМЖЕФАйЗжБШ=ВЮШќбЇЩњШЫЪ§ЁБЃЌМДПЩЧѓЕУВЮШќШЫЪ§ЃЌдйЧѓГіBЕШМЖШЫЪ§ЃЌВЙШЋЬѕаЮЭГМЦЭМЃЌМДПЩЃЛ
ЃЈ2ЃЉгЩCЕШМЖШЫЪ§ЁТВЮШќбЇЩњШЫЪ§ЃЌМДПЩЕУЕНmЕФжЕЃЌгЩ360ЁуЁСDЕШМЖЕФАйЗжБШЃЌМДПЩЕУЕНЁАDЕШМЖЁБЕФЩШаЮЕФдВаФНЧЃЛ
ЃЈ3ЃЉИљОнЬтвтЃЌСаГіБэИёЃЌЕУЕНЫљгаЕШПЩФмЕФНсЙћЃЌдйИљОнИХТЪЙЋЪНЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉИљОнЬтвтЕУЃК3ЁТ15%ЃН20ЃЈШЫЃЉЃЌ
ЁрВЮШќбЇЩњЙВ20ШЫЃЌ
BЕШМЖШЫЪ§гаЃК20ЉЃЈ3+8+4ЃЉЃН5ЃЈШЫЃЉЃЌ
ВЙШЋЬѕаЮЭМШчЯТЃК
ЃЈ2ЃЉCЕШМЖЕФАйЗжБШЮЊЃК![]() ЁС100%ЃН40%ЃЌМДЃКmЃН40ЃЌ
ЁС100%ЃН40%ЃЌМДЃКmЃН40ЃЌ
БэЪОЁАDЕШМЖЁБЕФЩШаЮЕФдВаФНЧЮЊЃК360ЁуЁС![]() ЃН72ЁуЃЌ
ЃН72ЁуЃЌ
ЙЪД№АИЮЊЃК40ЃЌ72ЃЛ
ЃЈ3ЃЉСаБэШчЯТЃК
Фа | ХЎ | ХЎ | |
Фа | ЃЈФаЃЌХЎЃЉ | ЃЈФаЃЌХЎЃЉ | |
ХЎ | ЃЈХЎЃЌФаЃЉ | ЃЈХЎЃЌХЎЃЉ | |
ХЎ | ЃЈХЎЃЌФаЃЉ | ЃЈХЎЃЌХЎЃЉ |
ЫљгаЕШПЩФмЕФНсЙћга6жжЃЌЦфжаЧЁКУЪЧвЛУћФаЩњКЭвЛУћХЎЩњЕФЧщПіга4жжЃЌ
ЁрPЃЈЧЁКУЪЧвЛУћФаЩњКЭвЛУћХЎЩњЃЉЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯC = 90ЁуЃЌ PЪЧCBБпЩЯвЛЖЏЕуЃЌСЌНгAPЃЌзїPQЁЭAPНЛABгкQ . вбжЊAC = 3cmЃЌBC = 6cmЃЌЩшPCЕФГЄЖШЮЊxcmЃЌBQЕФГЄЖШЮЊycm .

аЁЧрЭЌбЇИљОнбЇЯАКЏЪ§ЕФОбщЖдКЏЪ§yЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОП.
ЯТУцЪЧаЁЧрЭЌбЇЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
(1) АДееЯТБэжаздБфСПxЕФжЕНјааШЁЕуЁЂЛЭМЁЂВтСПЃЌЗжБ№ЕУЕНСЫyЕФМИзщЖдгІжЕЃЛ
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(ЫЕУїЃКВЙШЋБэИёЪБЃЌЯрЙиЪ§ОнБЃСєвЛЮЛаЁЪ§)
mЕФжЕдМЮЊЖрЩйcmЃЛ
(2)дкЦНУцжБНЧзјБъЯЕжаЃЌУшГівдВЙШЋКѓЕФБэИёжаИїзщЪ§жЕЫљЖдгІЕФЕу(x ЃЌy)ЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ

ЃЈ3ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃК
ЂйЕБy > 2ЪБЃЌаДГіЖдгІЕФxЕФШЁжЕЗЖЮЇЃЛ
ЂкШєЕуPВЛгыBЃЌCСНЕужиКЯЃЌЪЧЗёДцдкЕуPЃЌЪЙЕУBQ=BP?ЃЈжБНгаДНсЙћЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕ![]() ЩЯЕФЕу
ЩЯЕФЕу![]() КЭ
КЭ![]() ЃЌЖЈвхШчЯТЃКШє
ЃЌЖЈвхШчЯТЃКШє![]() ЩЯДцдкСНИіЕу
ЩЯДцдкСНИіЕу![]() ЃЌЪЙЕУЕу
ЃЌЪЙЕУЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌдђГЦ
ЃЌдђГЦ![]() ЮЊ
ЮЊ![]() ЕФвРИНЕуЃЎ
ЕФвРИНЕуЃЎ
ЃЈ1ЃЉЕБ![]() ЕФАыОЖЮЊ1ЪБ
ЕФАыОЖЮЊ1ЪБ
ЂйвбжЊЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдкЕу
ЃЌдкЕу![]() жаЃЌ
жаЃЌ![]() ЕФвРИНЕуЪЧ______ЃЛ
ЕФвРИНЕуЪЧ______ЃЛ
ЂкЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌШє
ЩЯЃЌШє![]() ЮЊ
ЮЊ![]() ЕФвРИНЕуЃЌЧѓЕу
ЕФвРИНЕуЃЌЧѓЕу![]() ЕФКсзјБъ
ЕФКсзјБъ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉ![]() ЕФдВаФдк
ЕФдВаФдк![]() жсЩЯЃЌАыОЖЮЊ1ЃЌжБЯп
жсЩЯЃЌАыОЖЮЊ1ЃЌжБЯп![]() гы
гы![]() жсЁЂ
жсЁЂ![]() жсЗжБ№НЛгкЕу
жсЗжБ№НЛгкЕу![]() ЃЌШєЯпЖЮ
ЃЌШєЯпЖЮ![]() ЩЯЕФЫљгаЕуЖМЪЧ
ЩЯЕФЫљгаЕуЖМЪЧ![]() ЕФвРИНЕуЃЌЧыЧѓГідВаФ
ЕФвРИНЕуЃЌЧыЧѓГідВаФ![]() ЕФКсзјБъ
ЕФКсзјБъ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
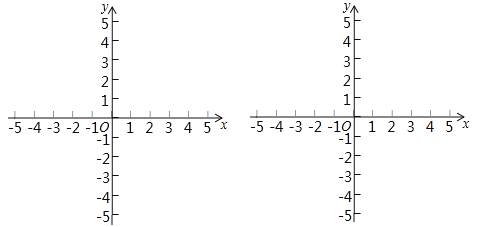
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАзюУРХЎНЬЪІЁБеХРіРђЃЌЮЊЧРОШСНУћбЇЩњЃЌвджТЫЋЭШИпЮЛНижЋЃЌЩчЛсИїНчЗзЗзЮЊЫ§ОшПюЃЌЮвЪаФГжабЇОХФъМЖвЛАрШЋЬхЭЌбЇВЮМгСЫОшПюЛюЖЏЃЌИУАрЭЌбЇОшПюЧщПіЕФВПЗжЭГМЦЭМШчЭМЫљЪОЃК

ЃЈ1ЃЉЧѓИУАрЕФзмШЫЪ§ЃЛ
ЃЈ2ЃЉНЋЬѕаЮЭМВЙГфЭъећЃЌВЂаДГіОшПюзмЖюЕФжкЪ§ЃЛ
ЃЈ3ЃЉИУАрЦНОљУПШЫОшПюЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
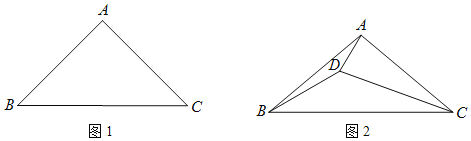
ЁОЬтФПЁПдкЁїABCжаЃЌAB=ACЃЌНЋЯпЖЮACШЦзХЕуCФцЪБеыа§зЊЕУЕНЯпЖЮCDЃЌа§зЊНЧЮЊІСЃЎ
ЃЈ1ЃЉШчЭМЃЌЁЯBAC=90ЁуЃЌІС=45ЁуЃЌЪдЧѓЕуDЕНБпABЃЌACЕФОрРыЕФБШжЕЃЛ
ЃЈ2ЃЉШчЭМЃЌЁЯBAC=100ЁуЃЌІС=20ЁуЃЌСЌНгADЃЌBDЃЌЧѓЁЯCBDЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCгыЁїDEFЖМЪЧЕШбќШ§НЧаЮЃЌЧвAB=AC=3ЃЌDE=DF=2ЃЌШєЁЯB+ЁЯE=90ЁуЃЌдђЁїABCгыЁїDEFЕФУцЛ§БШЮЊЃЈ ЃЉ

AЁЂ9ЃК4 BЁЂ3ЃК2 CЁЂ![]() :
:![]() DЁЂ3
DЁЂ3![]() :2
:2![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЕу
жаЃЌЕу![]() зјБъЪЧ
зјБъЪЧ![]() ЃЎЕБАбзјБъЯЕШЦЕу
ЃЎЕБАбзјБъЯЕШЦЕу![]() ЫГЪБеыбЁдё30ЁуЪБЃЌЕу
ЫГЪБеыбЁдё30ЁуЪБЃЌЕу![]() дка§зЊКѓЕФзјБъЯЕжаЕФзјБъЪЧ____ЃЛЕБАбзјБъЯЕШЦЕу
дка§зЊКѓЕФзјБъЯЕжаЕФзјБъЪЧ____ЃЛЕБАбзјБъЯЕШЦЕу![]() ФцЪБеыбЁдё30ЁуЪБЃЌЕу
ФцЪБеыбЁдё30ЁуЪБЃЌЕу![]() дка§зЊКѓЕФзјБъЯЕжаЕФзјБъЪЧ____ЃЎ
дка§зЊКѓЕФзјБъЯЕжаЕФзјБъЪЧ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
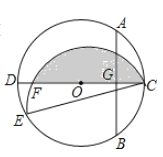
ЁОЬтФПЁПШчЭМЃЌCDЪЧЁбOЕФжБОЖЃЌABЪЧЁбOЕФЯвЃЌABЁЭCDЃЌДЙзуЮЊGЃЌOGЃКOC=3ЃК5ЃЌAB=8ЃЎЕуEЮЊдВЩЯвЛЕуЃЌЁЯECD=15ЁуЃЌНЋ![]() биЯвCEЗелЃЌНЛCDгкЕуFЃЌЭМжавѕгАВПЗжЕФУцЛ§=_________
биЯвCEЗелЃЌНЛCDгкЕуFЃЌЭМжавѕгАВПЗжЕФУцЛ§=_________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊМгПьЁАжЧЛлаЃдАЁБНЈЩшЃЌФГЪазМБИЮЊЪдЕубЇаЃВЩЙКвЛХњ![]() СНжжаЭКХЕФвЛЬхЛњЃЌОЙ§ЪаГЁЕїВщЗЂЯжЃЌУПЬз
СНжжаЭКХЕФвЛЬхЛњЃЌОЙ§ЪаГЁЕїВщЗЂЯжЃЌУПЬз![]() аЭвЛЬхЛњЕФМлИёБШУПЬз
аЭвЛЬхЛњЕФМлИёБШУПЬз![]() аЭвЛЬхЛњЕФМлИёЖр
аЭвЛЬхЛњЕФМлИёЖр![]() ЭђдЊЃЌЧвгУ
ЭђдЊЃЌЧвгУ![]() ЭђдЊЧЁКУФмЙКТђ
ЭђдЊЧЁКУФмЙКТђ![]() Ьз
Ьз![]() аЭвЛЬхЛњКЭ
аЭвЛЬхЛњКЭ![]() Ьз
Ьз![]() аЭвЛЬхЛњ.
аЭвЛЬхЛњ.
ЃЈ1ЃЉСаЖўдЊвЛДЮЗНГЬзщНтОіЮЪЬтЃКЧѓУПЬз![]() аЭКЭ
аЭКЭ![]() аЭвЛЬхЛњЕФМлИёИїЪЧЖрЩйЭђдЊЃП
аЭвЛЬхЛњЕФМлИёИїЪЧЖрЩйЭђдЊЃП
ЃЈ2ЃЉгЩгкашвЊЃЌОіЖЈдйДЮВЩЙК![]() аЭКЭ
аЭКЭ![]() аЭвЛЬхЛњЙВ
аЭвЛЬхЛњЙВ![]() ЬзЃЌДЫЪБУПЬз
ЬзЃЌДЫЪБУПЬз![]() аЭЬхЛњЕФМлИёБШдРДЩЯеЧ
аЭЬхЛњЕФМлИёБШдРДЩЯеЧ![]() ЃЌУПЬз
ЃЌУПЬз![]() аЭвЛЬхЛњЕФМлИёВЛБф.ЩшдйДЮВЩЙК
аЭвЛЬхЛњЕФМлИёВЛБф.ЩшдйДЮВЩЙК![]() аЭвЛЬхЛњ
аЭвЛЬхЛњ![]() ЬзЃЌФЧУДИУЪажСЩйЛЙашвЊЭЖШыЖрЩйЭђдЊЃП
ЬзЃЌФЧУДИУЪажСЩйЛЙашвЊЭЖШыЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com