
直线 与坐标轴分别交于
与坐标轴分别交于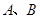 两点,动点
两点,动点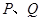 同时从
同时从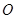 点出发,同时到达
点出发,同时到达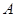 点,运动停止.点
点,运动停止.点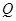 沿线段
沿线段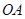 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点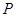 沿路线
沿路线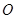 →
→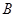 →
→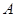 运动.
运动.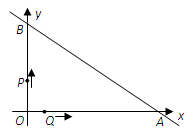
(1)直接写出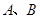 两点的坐标;
两点的坐标;
(2)设点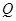 的运动时间为
的运动时间为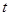 秒,
秒, 的面积为
的面积为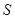 ,求出
,求出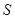 与
与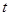 之间的函数关系式;
之间的函数关系式;
(3)当 时,求出点
时,求出点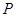 的坐标,并直接写出以点
的坐标,并直接写出以点 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点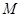 的坐标.
的坐标.
(1)A(8,0)B(0,6);(2)当0 时,
时,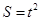 ,当
,当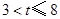 时,
时,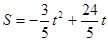 ;
;
(3)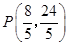 ,M1
,M1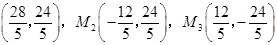
解析试题分析:(1)分别把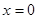 、
、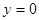 代入
代入 即可求得结果;
即可求得结果;
(2)先根据勾股定理求得AB的长,根据点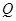 由
由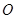 到
到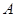 的时间可求得点
的时间可求得点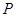 的速度,再分当
的速度,再分当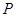 在线段
在线段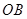 上运动(或0
上运动(或0 )时,当
)时,当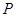 在线段
在线段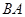 上运动(或
上运动(或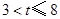 )时,两种情况,根据三角形的面积公式求解即可;
)时,两种情况,根据三角形的面积公式求解即可;
(3)把 代入(2)中的函数关系式即可求得点
代入(2)中的函数关系式即可求得点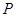 的坐标,再根据平行四边形的性质求解即可.
的坐标,再根据平行四边形的性质求解即可.
(1)A(8,0)B(0,6);
(2)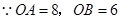
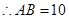
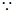 点
点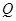 由
由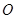 到
到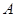 的时间是
的时间是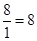 (秒)
(秒)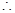 点
点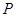 的速度是
的速度是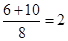 (单位/秒)
(单位/秒)
当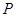 在线段
在线段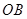 上运动(或0
上运动(或0 )时,
)时,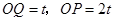 ,
,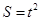
当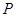 在线段
在线段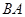 上运动(或
上运动(或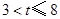 )时,
)时,
作 于点
于点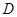 ,由
,由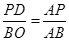 ,得
,得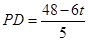 ,
,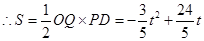 ;
;
(3)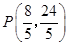 ,M1
,M1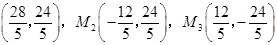
考点:动点的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.


科目:初中数学 来源:2011-2012学年浙江省台州市温岭市四校联考九年级(上)期中数学试卷(解析版) 题型:解答题
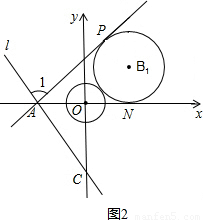
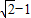 ,直线
,直线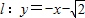 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.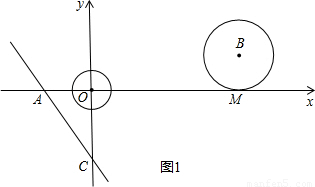
查看答案和解析>>
科目:初中数学 来源:2007-2008学年五校联考(第17周)九年级数学试卷(解析版) 题型:解答题
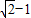 ,直线
,直线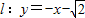 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.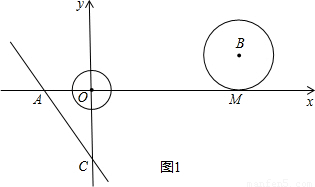

查看答案和解析>>
科目:初中数学 来源:2006-2007学年山东省济宁市九年级(上)期末联考数学试卷(解析版) 题型:解答题
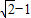 ,直线
,直线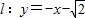 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M.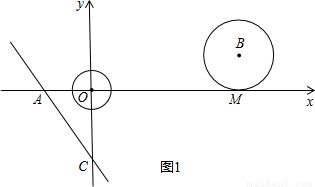

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(山东济宁卷)数学2(解析版) 题型:解答题
如图,直线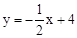 与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
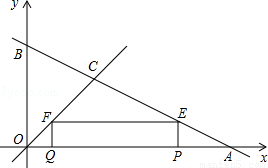
(1)求点P运动的速度是多少?
(2)当t为多少秒时,矩形PEFQ为正方形?
(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com