
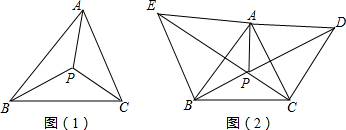
���� ��1�����ݵ������������ߺ�һ�����ʿ�֪��MBƽ�֡�ABC�����ABP=30�㣬ͬ����BAP=30�㣬���APB=120�㣬ͬ������á�APC����BPC�Ķ�����Ȼ��������жϣ�
��2���ɷ�����Ķ����֪��PAB=��PBC��Ȼ����֤����PAB=��PBC���ɣ�
��3����ͼ2��ʾ��������֤����ACE�ա�ABD�����1=��2���ɡ�3=��4�ɵõ���CPD=��5�� ���ɡ�CPD=60���֤����BPC=120�㣬Ȼ��֤����ADF�ס�CFP�������������ε����ʺ��ж�������֤����AFP�ס�CDF���ʴ˿ɵõ���APF=��ACD=60�㣬Ȼ�����á�APC=120�㣬����������á�APB=120�㣮
��� �⣺��1����ͼ1��ʾ��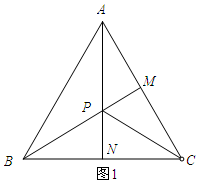
��AB=BC��BM��AC�����ߣ�
��MBƽ�֡�ABC��
ͬ����ANƽ�֡�BAC��PCƽ�֡�BCA��
�ߡ�ABCΪ�ȱ������Σ�
���ABP=30�㣬��BAP=30�㣮
���APB=120�㣮
ͬ������APC=120�㣬��BPC=120�㣮
��P�ǡ�ABC�ķ����㣮
�ʴ�Ϊ���ǣ�
��2���ߡ�PAB+��PBA=180��-��APB=60�㣬��PBC+��PBA=��ABC=60�㣬
���PAB=��PBC��
�֡ߡ�APB=��BPC=120�㣬
���ABP�ס�BCP��
��3����ͼ2��ʾ��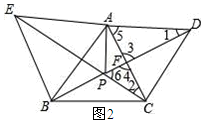
�١ߡ�ABE���ACD��Ϊ�ȱ������Σ�
���BAE=��CAD=60�㣬AE=AB��AC=AD��
���BAE+��BAC=��CAD+��BAC������EAC=��BAD��
�ڡ�ACE�͡�ABD�У�$\left\{\begin{array}{l}{AC=AD}\\{��EAC=��BAD}\\{EA=AB}\end{array}\right.$
���ACE�ա�ABD��SAS����
���1=��2��
�ߡ�3=��4��
���CPD=��6=��5=60�㣻
��֤�����ߡ�ADF�ס�CFP��
��AF•PF=DF•CF��
�ߡ�AFP=��CFD��
���AFP�ס�CDF��
���APF=��ACD=60�㣬
���APC=��CPD+��APF=120�㣬
���BPC=120�㣬
���APB=360��-��BPC-��APC=120�㣬
��P��Ϊ��ABC�ķ����㣮
���� ������Ҫ����������������ε��ۺ�Ӧ�ã��������ҪӦ���˵ȱ������ε����ʡ����������ε����ʡ�ȫ�������ε����ʺ��ж������������ε����ʺ��ж���֪ʶ��֤�á�5=��6����AFP�ס�CDF�ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ס���������Լ��ĩ�ǻ���ɽ���ס������˾����ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ����������⣺
�ס���������Լ��ĩ�ǻ���ɽ���ס������˾����ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ����������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �������������������Ƶ��ǣ�������
�������������������Ƶ��ǣ�������| A�� | A��B | B�� | A��C | C�� | B��C | D�� | A��B��C������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
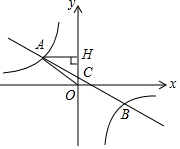 ��ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0����ͼ���뷴��������y=$\frac{k}{x}$��k��0����ͼ���ڵڶ������������ڵ�A��B���㣬��y�ύ��C�㣬��A��AH��y�ᣬ����ΪH��AH=4��tan��AOH=$\frac{4}{3}$����B������Ϊ��m��-2����
��ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��a��0����ͼ���뷴��������y=$\frac{k}{x}$��k��0����ͼ���ڵڶ������������ڵ�A��B���㣬��y�ύ��C�㣬��A��AH��y�ᣬ����ΪH��AH=4��tan��AOH=$\frac{4}{3}$����B������Ϊ��m��-2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
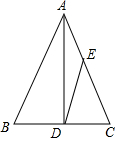 ��ͼ����֪AD�ǵ�����ABC�ױ�BC�ϵĸߣ�sinB=$\frac{4}{5}$����E��AC�ϣ���AE��EC=2��3����tan��ADE=��������
��ͼ����֪AD�ǵ�����ABC�ױ�BC�ϵĸߣ�sinB=$\frac{4}{5}$����E��AC�ϣ���AE��EC=2��3����tan��ADE=��������| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{2}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
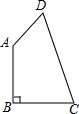 ��ͼ�����ı���ABCD�У�AB=BC=2��CD=3��DA=1����AB��BC��B��
��ͼ�����ı���ABCD�У�AB=BC=2��CD=3��DA=1����AB��BC��B���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com