
【题目】对某批乒乓球质量进行随机调查,结果如下表;
随机抽取的乒乓球数 | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
优等品数 | 7 | 16 | 43 | 81 | 164 | 410 | 820 |
优等频率 | 0.7 | 0.8 | 0.86 | 0.81 | 0.82 | 0.82 |
(1)填表格中的空为_______.
(2)根据上表估计,在这批乒乓球中任取一个球,它为优等品的概率大约是________.(保留两位小数点)
(3)学校需要500个乒乓球的优等品,那么可以推测出最有可能进这批货的乒乓球个数是多少合适?(结果保留整数)
科目:初中数学 来源: 题型:
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=∠CFF=45°
(1) 将△ADF绕点A顺时针旋转90 °,得到△ABG(如图1),求证:BE+DF=EF;
(2) 若直线EF与AB、AD的延长线分别交于点M、N(如图2),求证:![]()
(3) 将正方形改为长与宽不相等的矩形,其余条件不变(如图3),直接写出线段EF、BE、DF之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简再求值:
(1)(x+y)(xy)(4x3y4xy3)÷2xy,其中x=1,y=![]() .
.
(2)实数x满足x22x2=0,求代数式(2x1)2x(x+4)+(x3)(x+3)的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护环境,某区污水处理厂决定购买A,B两种型号污水处理设备10台,其中每台的价格、月处理污水量如下表.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.

(1)求a,b的值;
(2)某区污水处理厂决定购买污水处理设备的资金既不少于108万元也不超过110万元,问有几种购买方案?每月最多能处理污水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是我国北方某地一棵树在一天不同时刻拍下的五张图片,仔细观察后回答下列问题.
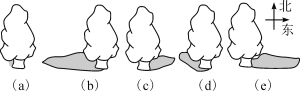
(1)说出这五张图片所对应的时间的先后顺序;
(2)根据生活经验,谈谈由早到晚该地物体影子的长短变化规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,求树的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某幼儿园计划购进一批甲、乙两种玩具,已知一件甲种玩具的价格与一件乙种玩具的价格的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的价格分别是多少元?
(2)该幼儿园计划用3500元购买甲、乙两种玩具,由于采购人员把甲、乙两种玩具的件数互换了,结果需4500元,求该幼儿园原计划购进甲、乙两种玩具各多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() .
.
(1)求该二次函数的解析式及点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴上的动点,
轴上的动点,
①求![]() 的最大值及对应的点
的最大值及对应的点![]() 的坐标;
的坐标;
②设![]() 是
是![]() 轴上的动点,若线段
轴上的动点,若线段![]() 与函数
与函数![]() 的图像只有一个公共点,求
的图像只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com