
【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
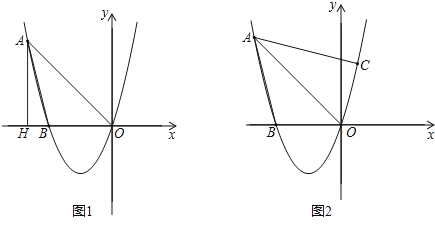
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
【答案】(1)![]() ;
;
(2)∠AOP=∠AOH+∠POH=45o+45o=90o;
(3)存在,直线AC解析式为![]()
【解析】试题分析:(1)根据已知点的坐标利用待定系数法确定二次函数的解析式即可;
(2)设点P坐标为(m,m2+3m),从而得到直线OA的解析式为y=-x,然后表示出点Q的坐标为(m,-m),进而表示出PQ=-m-(m2+3m)=-m2-4m,利用当四边形AHPQ为平行四边形时,PQ=AH=4得到-m2-4m=4,从而求得m的值,进而确定答案;
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,从而证得△AOD≌△AOB后表示点D坐标为(0,3),从而确定直线AC解析式,
试题解析:(1)由题意,得
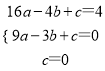 ,解得
,解得![]() .
.
∴抛物线的解析式为y=x2+3x;
(2)设点P坐标为(m,m2+3m),其中-4<m<0
∵点A(-4,4),
∴直线OA的解析式为y=-x,
从而点Q的坐标为(m,-m)
∴PQ=-m-(m2+3m)=-m2-4m,
当四边形AHPQ为平行四边形时,PQ=AH=4,
即-m2-4m=4,解得m=-2
此时点P坐标为(-2,-2)
∴∠AOP=∠AOH+∠POH=45°+45°=90°.
(3)设AC交y轴于点D,由点A(-4,4)得,∠AOB=∠AOD=45°,
∵∠CAO=∠BAO,AO=AO,
∴△AOD≌△AOB,
∴OD=OB=3,点D坐标为(0,3),
设直线AC解析式为y=px+q,则![]()
解得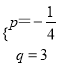 ,
,
∴直线AC解析式为y=![]() x+3
x+3


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“买一张电影票,座位号为偶数”是必然事件
B.若甲、乙两组数据的方差分别为s ![]() =0.3、s
=0.3、s ![]() =0.1,则甲组数据比乙组数据稳定
=0.1,则甲组数据比乙组数据稳定
C.一组数据2,4,5,5,3,6的众数是5
D.若某抽奖活动的中奖率为 ![]() ,则参加6次抽奖一定有1次能中奖
,则参加6次抽奖一定有1次能中奖
查看答案和解析>>
科目:初中数学 来源: 题型:
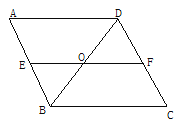
【题目】如图,AD∥BC,EF∥BC,BD平分∠ABC,图中与∠ADO相等的角有_______ 个,分别是___________.因为AB∥CD,EF∥AB,根据_____________________________,所以_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
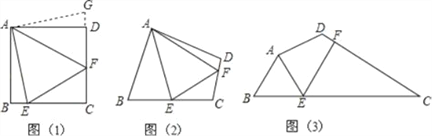
【题目】问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.
【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.
【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.
【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40(![]() ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解某个年级的学习情况,在这个年级抽取了50名学生,对某学科进行测试,将所得成绩(成绩均为整数)整理后,列出表格:
分组 | 50~59分 | 60~69分 | 70~79分 | 80~89分 | 90~99分 |
频率 | 0.04 | 0.04 | 0.16 | 0.34 | 0.42 |
(1)本次测试90分以上的人数有________人;(包括90分)
(2)本次测试这50名学生成绩的及格率是________;(60分以上为及格,包括60分)
(3)这个年级此学科的学习情况如何?请在下列三个选项中,选一个填在题后的横线上________.
A.好 B.一般 C.不好
查看答案和解析>>
科目:初中数学 来源: 题型:
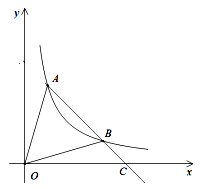
【题目】如图,A、B为反比例函数![]() 图像上的两点,A、B两点坐标分别为(
图像上的两点,A、B两点坐标分别为(![]() )、(
)、(![]() )(m<n),连接AB并延长交
)(m<n),连接AB并延长交![]() 轴于点C.
轴于点C.
(1)求![]() 的值;
的值;
(2)若B为AC的中点,求![]() 的值;
的值;
(3)过B点作OA的平行线交![]() 轴于(
轴于(![]() ,0),若
,0),若![]() 为整数,求
为整数,求![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
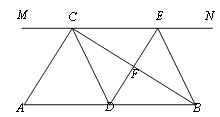
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时.
①求证:四边形BECD是菱形;
②当∠A为多少度时,四边形BECD是正方形?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com