
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=![]() x+2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=
x+2��x�ύ�ڵ�A����y�ύ�ڵ�C��������y=![]() x2+bx+c����A��C���㣬��x�����һ����Ϊ��B��
x2+bx+c����A��C���㣬��x�����һ����Ϊ��B��

��1���������ߵĺ�������ʽ��
��2����DΪֱ��AC�Ϸ���������һ���㣻
������BC��CD����ֱ��BD���߶�AC�ڵ�E����CDE�����ΪS1�� ��BCE�����ΪS2�� ��![]() �����ֵ��
�����ֵ��
�ڹ���D��DF��AC������Ϊ��F������CD���Ƿ���ڵ�D��ʹ�á�CDF�е�ij����ǡ�õ��ڡ�BAC��2���������ڣ����D�ĺ����ꣻ�������ڣ���˵������
���𰸡���1��![]() ��2���ٵ�a=2ʱ��
��2���ٵ�a=2ʱ�� ![]() �����ֵ��
�����ֵ��![]() ����2��
����2��![]()
�������������������1����������õ�A����4��0����C��0��2������y=��![]() x2+bx+c�����ǵõ����ۣ���2������ͼ����y=0���ⷽ�̵õ�x1=��4��x2=1�����B��1��0������D��DM��x����M����B��BN��x�ύ��AC��N���������������ε����ʼ��ɵõ����ۣ��ڸ��ݹ��ɶ������涨���õ���ABC���ԡ�ACBΪֱ�ǵ�ֱ�������Σ�ȡAB���е�P�����P����
x2+bx+c�����ǵõ����ۣ���2������ͼ����y=0���ⷽ�̵õ�x1=��4��x2=1�����B��1��0������D��DM��x����M����B��BN��x�ύ��AC��N���������������ε����ʼ��ɵõ����ۣ��ڸ��ݹ��ɶ������涨���õ���ABC���ԡ�ACBΪֱ�ǵ�ֱ�������Σ�ȡAB���е�P�����P����![]() ��0�����õ�PA=PC=PB=
��0�����õ�PA=PC=PB=![]() ������x���ƽ���߽�y����R����AC��������G�����һ����ͼ����DCF=2��BAC=��DGC+��CDG�����������FDC=2��BAC����ֱ�������μ��ɵõ����ۣ�
������x���ƽ���߽�y����R����AC��������G�����һ����ͼ����DCF=2��BAC=��DGC+��CDG�����������FDC=2��BAC����ֱ�������μ��ɵõ����ۣ�
�����������1���⣺���������A����4��0����C��0��2����
��������y=�� ![]() x2+bx+c����A��C���㣬
x2+bx+c����A��C���㣬
�� ![]() ��
��
�� ![]() ��
��
��y=�� ![]() x2��
x2�� ![]() x+2
x+2
��2���⣺����ͼ��
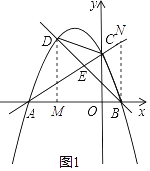
��y=0��
�ੁ ![]() x2��
x2�� ![]() x+2=0��
x+2=0��
��x1=��4��x2=1��
��B��1��0����
��D��DM��x����M����B��BN��x�ύ��AC��N��
��DM��BN��
���DME�ס�BNE��
�� ![]() =
= ![]() =
= ![]() ��
��
��D��a��=�� ![]() a2��
a2�� ![]() a+2����
a+2����
��M��a�� ![]() a+2����
a+2����
��B��1.0����
��N��1�� ![]() ����
����
�� ![]() =
= ![]() =
= ![]() ��a+2��2+
��a+2��2+ ![]() ��
��
�൱a=2ʱ�� ![]() �����ֵ��
�����ֵ�� ![]() ��
��
�ڡ�A����4��0����B��1��0����C��0��2����
��AC=2 ![]() ��BC=
��BC= ![]() ��AB=5��
��AB=5��
��AC2+BC2=AB2 ��
���ABC���ԡ�ACBΪֱ�ǵ�ֱ�������Σ�ȡAB���е�P��
��P���� ![]() ��0����
��0����
��PA=PC=PB= ![]() ��
��
���CPO=2��BAC��
��tan��CPO=tan��2��BAC��= ![]() ��
��
����x���ƽ���߽�y����R����AC���ӳ�����G��
���һ����ͼ��
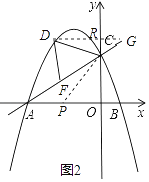
���DCF=2��BAC=��DGC+��CDG��
���CDG=��BAC��
��tan��CDG=tan��BAC= ![]() ��
��
�� ![]() ��
��
��D��a���� ![]() a2��
a2�� ![]() a+2����
a+2����
��DR=��a��RC=�� ![]() a2��
a2�� ![]() a��
a��
�� ![]() ��
��
��a1=0����ȥ����a2=��2��
��xD=��2��
����������FDC=2��BAC��
��tan��FDC= ![]() ��
��
��FC=4k��
��DF=3k��DC=5k��
��tan��DGC= ![]() =
= ![]() ��
��
��FG=6k��
��CG=2k��DG=3 ![]() k����
k����
��RC= ![]() k��RG=
k��RG= ![]() k��
k��
DR=3 ![]() k��
k�� ![]() k=
k= ![]() k��
k��
�� ![]() =
= ![]() =
= ![]() ��
��
��a1=0����ȥ����a2= ![]() ��
��
��D�ĺ�����Ϊ��2�� ![]() ��
��


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ƽ���ߣ��ҽ�
��ƽ���ߣ��ҽ�![]() ��
��![]() �����
�����![]() ����
����![]() �ij��� ��
�ij��� ��

A.2B.4C.6D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ���Ƚ�
��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ���Ƚ�![]() ����ƽ��3����λ��������ƽ��1����λ��
����ƽ��3����λ��������ƽ��1����λ��![]() ��
��![]() ��
��![]() ����
����![]() ��Գƣ�
��Գƣ�

��1������![]() ��
��![]() ��
��
��2����![]() ����ȷ��һ��
����ȷ��һ��![]() ��ʹ
��ʹ![]() ��ֵ��С���������
��ֵ��С���������![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����M��N�ֱ���������ABCD�ı�CD��CB�ϵĶ��㣬����DM=CN��AM��DN�ཻ�ڵ�E������CE���������εı߳�Ϊ2�����߶�CE����Сֵ��______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���;�Aλ���Ϳ�P��ƫ��75�㷽�������ܵ�AP=12km��һ�½��;�Bλ�ڵ�P�ı�ƫ��75�㷽����λ�ڵ�A�ı�ƫ��15�㷽��
��1�����PBA��
��2����A��B��ľ��룻
��3��Ҫ��AP��ѡ��һ��֧�ܵ����ӵ�C��ʹ�ӵ�B����C����֧���ܵ���̣�����ʱBC�ij���������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����С��Ϊ�˽�ͬѧ�Ƕ�ѧУ�������ܲ������ϲ���̶�,��ȡ����ѧ�����е���.�������ÿ��ѧ����A(�dz�ϲ��)��B(�Ƚ�ϲ��)��C(һ��)��D(��ϲ��)�ĸ��ȼ��Ի����.ͼ1��ͼ2�Ǹ�С��ɼ����ݺ���Ƶ�����ͳ��ͼ.��ȷ������ͳ��ͼ����ȷ�ģ�������ͳ��ͼ����һ�������Ҳ�������.�������ͳ��ͼ�ṩ����Ϣ������������⣺

(1)�˴ε����ѧ������Ϊ___��
(2)����ͳ��ͼ�д��ڴ������___(��A. B.C�е�һ��)������ͼ�м��Ը�����
(3)��ͼ2�в�������ͳ��ͼ�в������IJ��֣�
(4)�����У��600��ѧ������ô�Դ˻���dz�ϲ���������Ƚ�ϲ������ѧ�����ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������BCE�У���A�DZ�BE��һ�㣬��ABΪֱ���ġ�O��CE�����ڵ�D��AD��OC����FΪOC���O�Ľ��㣬����AF.
��1����֤��CB�ǡ�O�����ߣ�
��2������ECB=60����AB=6����ͼ����Ӱ���ֵ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����O����ֱ��CD�ĶԳƵ�ΪE������DE��CE��

��1����֤���ı���ODECΪ���Σ�
��2������OE����BC��2![]() ����OE�ij���
����OE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����E��F�ֱ���ֱ��AB��CD�ϣ���G��H����ֱ��֮�䣬�߶�EF��GH�ཻ�ڵ�O�����С�AEF+��CFE��180�㣬��AEF����1����2������ͼ����ȵĽǹ��У�������

A. 5��B. 6��C. 7��D. 8��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com