
分析 (1)设水果有x箱,则蔬菜有(x-800)箱,根据“蔬菜和水果共3200箱”列出方程并解答;
(2)设租用甲种货车a辆,则租用乙种货车(8-a)辆.依据“每辆甲种货车最多可装水果400箱和蔬菜100箱,每辆乙种货车最多可装水果和蔬菜各200箱”列出不等式组,求其整数解即可;
(3)利用(2)的设计方案分别计算它们的运费,再比较大小即可得到答案.
解答 解:(1)设水果有x箱,则蔬菜有(x-800)箱,则
x+(x-800)=3200,
解得x=2000,
则x-800=1200.
答:水果和蔬菜分别为2000箱和1200箱.
(2)设租用甲种货车a辆,则租用乙种货车(8-a)辆.根据题意,得
$\left\{\begin{array}{l}{400a+200(8-a)≥2000}\\{100a+200(8-a)≥1200}\end{array}\right.$,
解得:2≤a≤4.
因为a为整数,
所以a=2或3或4,安排甲、乙两种货车时有3种方案.
设计方案分别为:①甲车2辆,乙车6辆;②甲车3辆,乙车5辆;③甲车4辆,乙车4辆;
(3)3种方案的运费分别为:
①2×4000+6×3600=29600元;
②3×4 000+5×3600=30000元;
③4×4000+4×3600=30400元.
故方案①的运费最少,最少运费是29600元.
所以,运输部门应选择甲车2辆,乙车6辆,可使运费最少,最少运费是29600元.
点评 本题考查了一元一次方程的应用,一元一次不等式组的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系.


科目:初中数学 来源: 题型:解答题
| 类别 | 频数 | 频率 |
| 助人为乐美德少年 | a | 0.20 |
| 自强自立美德少年 | 3 | b |
| 孝老爱亲美德少年 | 7 | 0.35 |
| 诚实守信美德少年 | 6 | 0.32 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 2 | C. | 0 | D. | -8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-1 | B. | m>$\frac{1}{2}$ | C. | -1<m<$\frac{1}{2}$ | D. | 0<m<$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
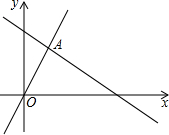 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为( )| A. | x≤3 | B. | x≥3 | C. | x≤$\frac{3}{2}$ | D. | x≥$\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com