
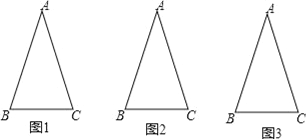
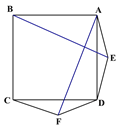
【题目】如图,△ABC中,AB=AC,∠A=36°,称满足此条件的三角形为黄金等腰三角形.请完成以下操作:(画图不要求使用圆规,以下问题所指的等腰三角形个数均不包括△ABC)
(1)在图1中画1条线段,使图中有2个等腰三角形,并直接写出这2个等腰三角形的顶角度数分别是 度和 度;
(2)在图2中画2条线段,使图中有4个等腰三角形;
(3)继续按以上操作发现:在△ABC中画n条线段,则图中有 个等腰三角形,其中有 个黄金等腰三角形.
【答案】(1)108,36;(2)作图见解析;(3)2n,n.
【解析】试题分析:(1)利用等腰三角形的性质以及∠A的度数,进而得出这2个等腰三角形的顶角度数;
(2)利用(1)种思路进而得出符合题意的图形;
(3)利用当1条直线可得到2个等腰三角形;当2条直线可得到4个等腰三角形;当3条直线可得到6个等腰三角形,进而得出规律求出答案.
试题解析:(1)如图1所示:∵AB=AC,∠A=36°,
∴当AE=BE,则∠A=∠ABE=36°,则∠AEB=108°,
则∠EBC=36°,
∴这2个等腰三角形的顶角度数分别是108度和36度;
故答案为:108,36;
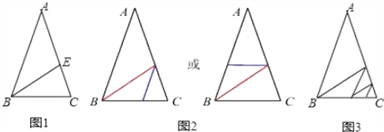
(2)如图2所示:
(3)如图3所示:当1条直线可得到2个等腰三角形;
当2条直线可得到4个等腰三角形;
当3条直线可得到6个等腰三角形;
…
∴在△ABC中画n条线段,则图中有2n个等腰三角形,其中有n个黄金等腰三角形.
故答案为:2n,n.


科目:初中数学 来源: 题型:
【题目】某人存入5000元参加三年期教育储蓄(免征利息税),本息共得5417元,那么这种储蓄的年利率为
A.2.22%B.2.58%C.2.78% D.2.38%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,牧童在A处放牛,其家在C处,A、C到河岸L的距离分别为AB=2km,CD=4km且,BD=8km。
(1)牧童从A处将牛牵到河边P处饮水后再回到家C,试确定P在何处,所走路程最短?请在图中画出饮水的位置(保留作图痕迹),不必说明理由。
(2)求出(1)中的最短路程。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角△ABC中,AB=AC,∠BAC=90°,小敏将一块三角板中含45°角的顶点放在A上,从AB边开始绕点A逆时针旋转一个角α,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E.
(1)小敏在线段BC上取一点M,连接AM,旋转中发现:若AD平分∠BAM,则AE也平分∠MAC.请你证明小敏发现的结论;
(2)当0°<α≤45°时,小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系:BD2+CE2=DE2.同组的小颖和小亮随后想出了相同的方法进行解决:将△ABD沿AD所在的直线对折得到△ADF(如图2);请证明小敏的发现的是正确的.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,且DH=CH,连结BD.
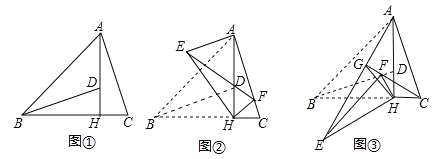
(1)求证:BD=AC;
(2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.
①如图②,当点F落在AC上时,(F不与C重合),若BC=4,tanC=3,求AE的长;
②如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.
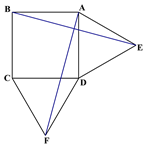

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com