
����Ŀ��һ����¼Ƭ�����˹��ڵ�������ϼ�һ���йص���Ԥ������ۣ�һλר��ָ��������δ��20�꣬A���з�������Ļ���������֮����
����λר�ҵij����������ĸ��ƶϣ�
��![]() ��20��13.3�����Խ���13����14��䣬A���лᷢ��һ�ε���
��20��13.3�����Խ���13����14��䣬A���лᷢ��һ�ε���
��![]() ����50%������δ��20�꣬A����һ����������
����50%������δ��20�꣬A����һ����������
����δ��20�꣬A���з�������Ŀ����Դ��ڲ���������Ŀ����ԣ�
������ȷ����δ��20�꣬A�����Ƿ�ᷢ������
���к������ǣ��� ����
A. �٢� B. �ڢ� C. �ڢ� D. �ۢ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����У���ƻ������Ϊ1800m2����������̻������żס����������̶����.��֪��ÿ��������̻���������Ҷ�ÿ��������̻��������2���������ڶ���������Ϊ400 m2������̻�ʱ���ӱ��Ҷ�����4��.
��1����ס��������̶�ÿ��������̻�������ֱ��Ƕ���m2��
��2����ѧУÿ���踶���ӵ��̻�������0.4��Ԫ���Ҷ�Ϊ0.25��Ԫ��Ҫʹ��ε��̻��ܷ��ò�����8��Ԫ������Ӧ���żӹ��������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��Բ�Ľ�Ϊ45�������ֽ�����һ���߳�Ϊ1�������Σ�������ֽ��������cm2����������У� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�����ڣ�ij����վ�ÿ��������������ÿ�������Ҫ��ʱ���ŶӵȺ��Ʊ�������鷢�֣��ڳ�վ��ʼ��Ʊʱ����640���ŶӼ�Ʊ����Ʊ��ʼ�������ÿͼ���ǰ���ŶӼ�Ʊ��վ�����ÿͰ��̶����ٶ����ӣ���Ʊ�ڼ�Ʊ���ٶ�Ҳ�ǹ̶��ģ���Ʊʱ��ÿ���Ӻ��������ŶӼ�Ʊ��վ16�ˣ�ÿ����ÿ����Ʊ�ڼ�Ʊ14�ˣ���֪��Ʊ��ǰa����ֻ������������Ʊ�ڣ�ijһ������ŶӵȺ��Ʊ������y���ˣ����Ʊʱ��x�����ӣ��Ĺ�ϵ��ͼ��ʾ��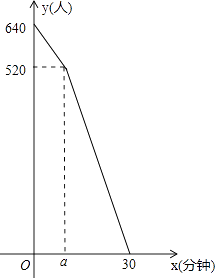
��1����a��ֵ��
��2�����Ʊ����20����ʱ�������ŶӵȺ��Ʊ���ÿ�������
��3����Ҫ�ڿ�ʼ��Ʊ��15�������������Ŷӵ��ÿͶ��ܼ�Ʊ��վ���Ա������վ���ÿ��浽��죬�ʼ�Ʊһ��ʼ������Ҫͬʱ���ż�����Ʊ�ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
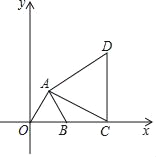
����Ŀ����ƽ��ֱ������ϵ�У���AOBΪ�ȱ������Σ�B��2��0����ֱ��l��y=kx+b������B����C��x���������ϵ�һ���㣬���߶�ACΪ���ڵ�һ�������ȱ���ACD��
��1��ֱ��д����A�����꣺A���� ������ ��������ֱ��l������Aʱ����ֱ��BA�ı���ʽ��
��2����ֱ��l������Dʱ��ֱ����y���ཻ�ڵ�F�����ŵ�C�ı仯����F��λ���Ƿ����仯����û�б仯�������ʱ��F�����꣮�����б仯����˵�����ɣ�
��3����ֱ�����߶�OA�ཻ���Eʱ�����ֱ��l����AOB�������Ϊ1��2�����֣������ʱ��E�����꣮
��4������C������Ϊ��4��0��ʱ��ֱ��l���߶�AD�н��㣬��ֱ��д����ʱk��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y=ax2��5ax+4a��x�ύ��A��B��A����B�����ࣩ��y�ύ�ڵ�C��
��1����ͼ1������AC��BC������ABC�����Ϊ3ʱ���������ߵĽ���ʽ��
��2����ͼ2����PΪ����������������һ�㣬����PC������BCP=2��ABCʱ�����P�ĺ����ꣻ
��3����ͼ3���ڣ�2���������£���F��AP�ϣ�����P��PH��x����H�㣬��K��PH���ӳ����ϣ�AK=KF����KAH=��FKH��PF=��4 ![]() a������KB���ӳ����������ڵ�Q����PQ�ij���
a������KB���ӳ����������ڵ�Q����PQ�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С��ͬѧ�����һ�ô����ĸ߶ȣ���վ��B�������������������Ϊ30�㣬���������ķ���ǰ��4m���������Ϊ60�㣬��֪С��ͬѧ���ߣ�AB��Ϊ1.6m����������ĸ߶�Ϊ�� ���������ȷ��0.1m�� ![]() ��1.73����
��1.73����
A.3.5m
B.3.6m
C.4.3m
D.5.1m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ����
����![]() ��������
��������![]() ��0������
��0������![]() ��������
��������![]() ��0����
��0����
��1����![]() ��ֵ��
��ֵ��
��2������![]() ��
��![]() ��
��![]() ���ǵڶ������ڵ�ֱ���ϵ�һ�����㣮����
���ǵڶ������ڵ�ֱ���ϵ�һ�����㣮����![]() �˶������У���д��
�˶������У���д��![]() �����
�����![]() ��
��![]() �ĺ�����ϵʽ����д���Ա���
�ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��̽������![]() �˶���ʲôλ��ʱ��
�˶���ʲôλ��ʱ��![]() �����Ϊ
�����Ϊ![]() ����˵�����ɣ�
����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����м�����̣����ֹ��ɣ����ù��ɲ��벢���㣺
1+2=![]() =3��1+2+3=
=3��1+2+3=![]() =6��1+2+3+4=
=6��1+2+3+4=![]() =10��1+2+3+4+5=
=10��1+2+3+4+5=![]() =15����
=15����
��1�����룺1+2+3+4+��+n=������
��2�������������ɼ��㣺1+2+3+4+��+200��
��3�����Լ��㣺3+6+9+12+��3n�Ľ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com