
【题目】已知M、N直线l上两点,MN=20,O、P为线段MN上两动点,过O、P分别作长方形OABC与长方形PDEF(如图),其中,两边OA、PF分别在直线l上,图形在直线l的同侧,且OA=PF=4,CO=DP=3,动点O从点M出发,以1单位/秒的速度向右运动;同时,动点P从点N出发,以2单位/秒的速度向左运动,设运动的时间为t秒.
(1)若t=2.5秒,求点A与点F的距离;
(2)求当t为何值时,两长方形重叠部分为正方形;
(3)运动过程中,在两长方形没有重叠部分前,若能使线段AB、BC、AF的长构成三角形,求t的取值范围.

【答案】(1)4.5;(2)当t分别为5秒、![]() 秒时,两长方形重叠部分为正方形;(3)t的取值范围为
秒时,两长方形重叠部分为正方形;(3)t的取值范围为![]()
【解析】
(1)求出MA,NF的值即可判断;
(2)分两种情形:ABEF是正方形;OCDP是正方形.分别求解即可解决问题;
(3)求出相遇前AF=7或1时的时间即可解决问题.
解:(1)当t=2.5秒时,MA=MO+OA=2.5+4=6.5,
NF=NP+PF=2.5×2+4=9,
∴AF=20﹣6.5﹣9=4.5.
(2)第一次重叠部分为正方形ABEF(如图)此时FA=3,
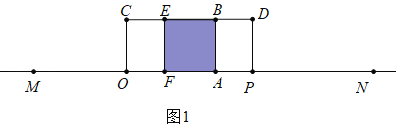
MA=t+4,NF=2t+4,
∴(t+4)+(2t+4)﹣20=3,
∴t=5.
第二次重叠部分为正方形PDCO(如图)此时OP=3,
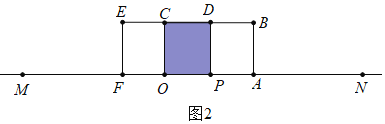
OM=t,PN=2t,
∴20﹣t﹣2t=3,
∴t=![]() ,
,
∴当t分别为5秒、![]() 秒时,两长方形重叠部分为正方形;
秒时,两长方形重叠部分为正方形;
(3)∵线段AB、BC、AF的长构成三角形,AB=3,BC=4,
∴1<AF<7,
重叠前AF=7,则有20﹣(t+4)﹣(2t+4)=7,
解得t=![]() ;
;
AF=1,则有20﹣(t+4)﹣(2t+4)=1,
解得t=![]() ,
,
∴t的取值范围为![]() .
.


科目:初中数学 来源: 题型:
【题目】下面是小东设计的“作平行四边形ABCD,使∠B=45°,AB=2cm,BC=3cm”的作图过程.
(1)作法:如图,①画∠B=45°;

②在∠B的两边上分别截取BA=2cm,BC=3cm.
③以点A为圆心,BC长为半径画弧,以点![]() 为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.
为圆心,AB长为半径画弧,两弧相交于点D;则四边形ABCD为所求的平行四边形.
根据小东设计的作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() _______,
_______,![]() _______,
_______,
∴四边形ABCD为所求的平行四边形.(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装店10月份以每套500元的进价购进一批羽绒服,当月以标价销售,销售额14000元,进入11月份搞促销活动,每件降价50元,这样销售额比10月份增加了5500元,售出的件数是10月份的1.5倍.
(1)求每件羽绒服的标价是多少元;
(2)进入12月份,该服装店决定把剩余的羽绒服按10月份标价的八折销售,结果全部卖掉,而且这批羽绒服总获利不少于12700元,问这批羽绒服至少购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
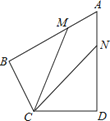
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,若
,若![]() ,
,![]() ,
,
①四边形![]() 是平行四边形;
是平行四边形;
②![]() 是等腰三角形;
是等腰三角形;
③四边形![]() 的周长是
的周长是![]() ;
;
④四边形![]() 的面积是16.
的面积是16.
则以上结论正确的是![]()
![]()

A. ①②③B. ①②④C. ①③④D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
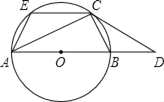
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,过C点的切线与AB的延长线交于点D,CE∥AB交⊙O于点E,连接AC、BC、AE.
(1)求证:①∠DCB=∠CAB;②CDCE=CBCA;
(2)作CG⊥AB于点G.若tan∠CAB=![]() (k>1),求
(k>1),求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c的图象开口向上,且经过点A(0,![]() ).
).
(1)若此函数的图象经过点(1,0)、(3,0),求此函数的表达式;
(2)若此函数的图象经过点B(2,﹣![]() ),且与x轴交于点C、D.
),且与x轴交于点C、D.
①填空:b=_____(用含α的代数式表示);
②当CD2的值最小时,求此函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
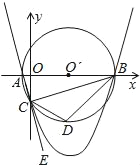
【题目】如图,已知点A的坐标是(﹣1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC,BC,过A,B,C三点作抛物线.
(1)求抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,连接BD,求直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD?如果存在,请求出点P的坐标;如果不存在,请说明理由.
第三问改成,在(2)的条件下,点P是直线BC下方的抛物线上一动点,当点P运动到什么位置时,△PCD的面积是△BCD面积的三分之一,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天,一蔬菜经营户用90元钱按批发价从蔬菜批发市场买了西红柿和豆角共50kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如下表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.0 | 1.5 |
零售价(单位:元/kg) | 2.9 | 2.6 |
如果西红柿和豆角全部以零售价售出,他当天卖这些西红柿和豆角赚了多少元钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com