
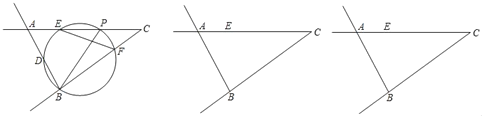
【题目】如图,在锐角△ABC中,BC=10,AC=11,△ABC的面积为33,点P是射线CA上一动点,以BP为直径作圆交线段AC于点E,交射线BA于点D,交射线CB于点F.
(1)当点P在线段AC上时,若点E为![]() 中点,求BP的长.
中点,求BP的长.
(2)连结EF,若△CEF为等腰三角形,求所有满足条件的BP值.
(3)将DE绕点D顺时针旋转90°,当点E的对应点E'恰好落在BC上时,记△DBE'的面积为S1,△DPE的面积S2,则![]() 的值为 .(直接写出答案即可)
的值为 .(直接写出答案即可)
【答案】(1)![]() ;(2)
;(2)![]() 或10或2
或10或2![]() ;(3)
;(3)![]() .
.
【解析】
(1)先利用面积求高BE,再由勾股定理求AB、AE、CE,再根据全等三角形判定和性质求得PB;
(2)△CEF为等腰三角形,可以分三种情况:①CF=EF,过F作FG⊥AC于点G,连接PF,利用相似三角形性质即可得到答案;②EF=CE,过E作EG⊥CB于G,连接EF、BP,利用全等三角形判定和性质即可;③CE=CF,利用全等三角形判定、性质和勾股定理即可;
(3)过点E作EM⊥DP于点M,过E′作E′G⊥AC于点G,作E′N⊥AB于点N,过D作DF⊥AC于点F,作DH⊥E′G于点H,依次证明:DFGH是矩形,△DEF≌△DE′H(AAS),△E′DN≌△EDM(AAS),再运用由相似三角形性质和解直角三角形知识即可.
解:(1)如图1,连接BE、DE,∴BP为直径,
∴∠BEC=∠BEA=90°
∵BC=10,AC=11,△ABC的面积为33,
∴![]() ACBE=33
ACBE=33
∴BE=6
∴CE=![]() =8
=8
∴AE=AC﹣CE=3
∴AB=![]() =3
=3![]()
∵点E为![]() 中点
中点
∴∠ABE=∠PBE
∵BE=BE
∴△ABE≌△PBE(ASA)
∴BP=AB=3![]() ;
;
(2)∵△CEF为等腰三角形,可以分三种情况:
①CF=EF,如图2,过F作FG⊥AC于点G,连接PF,
∵BP是直径
∴∠BFP=∠CFP=∠CGF=∠CEB=90°
∴EG=CG=![]() CF=4
CF=4
∵FG∥BE
∴△CFG∽△CBE∽△CPF
∴![]() =
=![]() =
=![]() ,
,![]() =
=![]()
∴![]() ,即CF=5,
,即CF=5,
∴![]() =
=![]() ,即CP=
,即CP=![]() ,
,
∴EP=CE﹣CP=8﹣![]() =
=![]() ,
,
∴BP=![]() =
= =
=![]() ;
;
②EF=CE,如图3,过E作EG⊥CB于G,连接EF、BP,则CG=GF
∴∠EFG=∠C
∵![]() =
=![]()
∴∠BPE=∠EFG
∴∠C=∠BPE
∵∠CEB=∠PEB=90°,BE=BE
∴△CBE≌△PBE(AAS)
∴BP=BC=10
③CE=CF,如图4,连接EF、BP、BE、AF,
∵BP为直径
∴∠AFB=∠AEB=90°
∵∠C=∠C
∴△CEB≌△CFP(ASA)
∴CP=CB=10
∴PE=2
∴BP=![]() =
=![]() =2
=2![]()
综上所述,满足条件的BP值为:![]() 或10或
或10或![]() .
.
(3)如图5,过点E作EM⊥DP于点M,过E′作E′G⊥AC于点G,作E′N⊥AB于点N,过D作DF⊥AC于点F,作DH⊥E′G于点H,
∵DF⊥AC,DH⊥E′G,E′G⊥AC
∴∠DFE=∠DHE′=∠E′GF=90°
∴DFGH是矩形,
∴GH=DF FG=DH∠FDH=90°
∴∠EDF+∠EDH=90°
∵∠EDH+∠
∴∠EDF=∠E′DH
∵DE=DE′
∴△DEF≌△DE′H(AAS)
∴DF=DH,EF=E′H
∵DF∥BE
∴![]() =
=![]() =
=![]() ,设AF=m,则:DF=DH=GH=FG=2m,EF=E′H=3﹣m,
,设AF=m,则:DF=DH=GH=FG=2m,EF=E′H=3﹣m,
∴E′G=m+3,AG=3m,CG=CA﹣AG=11﹣3m,
∵tan∠C=![]() =
=![]() =
=![]() =
=![]() ,即:4E′G=3CG,
,即:4E′G=3CG,
∴4(m+3)=3(11﹣3m),解得:m=![]() ,
,
EF=3﹣![]() =
=![]() ,DF=2×
,DF=2×![]() =
=![]() ,
,
∵BP是直径,
∴∠E′DN+∠E′DP=90°,
∵∠E′DP+∠EDM=90°
∴∠E′DN=∠EDM
∴△E′DN≌△EDM(AAS)
∴E′N=EM
∴![]() =
=![]() =
=![]() =tan∠BPD
=tan∠BPD
∵![]()
∴∠BED=∠BPD
∵DF∥BE
∴∠BED=∠EDF
∴∠BPD=∠EDF
∴tan∠BPD=tan∠EDF=![]() =
=![]()
∴![]() =
=![]() ,
,
故答案为:![]() .
.







科目:初中数学 来源: 题型:
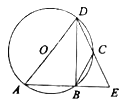
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() ,点
,点![]() 、
、![]() 在⊙
在⊙![]() 上,
上,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,且
,且![]() ,
,![]() ,有以下结论:①
,有以下结论:①![]() ;②劣弧
;②劣弧![]() 的长为
的长为![]() ;③点
;③点![]() 为
为![]() 的中点;④
的中点;④![]() 平分
平分![]() ,以上结论一定正确的是______.
,以上结论一定正确的是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2mx+(m2﹣1)(m是常数).
(1)若它的图象与x轴交于两点A,B,求线段AB的长;
(2)若它的图象的顶点在直线y=![]() x+3上,求m的值.
x+3上,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年1月,温州轨道交通![]() 线正式运营,
线正式运营,![]() 线有以下4种购票方式:
线有以下4种购票方式:
A.二维码过闸 B.现金购票 C.市名卡过闸 D.银联闪付
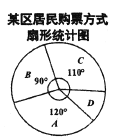
(1)某兴趣小组为了解最受欢迎的购票方式,随机调查了某区的若干居民,得到如图所示的统计图,已知选择方式D的有200人,求选择方式A的人数.
(2)小博和小雅对A,B,C三种购票方式的喜爱程度相同,随机选取一种方式购票,求他们选择同一种购票方式的概率.(要求列表或画树状图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:其中方案所示图形是顶点在原点的抛物线的部分,方案二所示的图形是射线, 设推销员销售产品的数量为![]() (件),付给推销员的月报酬为
(件),付给推销员的月报酬为![]() (元),
(元),
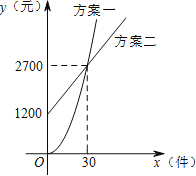
(1)请直接写出两种方案中![]() 关于
关于![]() 的函数关系式:方案一: ,方案二: ;
的函数关系式:方案一: ,方案二: ;
(2)当销售量达到多少件时,两种方案的月报酬差额将达到![]() 元?
元?
(3)若公司决定改进“方案二”:基本工资![]() 元,每销售件产品再增加报酬
元,每销售件产品再增加报酬![]() 元,当推销员销售量达到
元,当推销员销售量达到![]() 件时,方案二的月报酬不低于方案一的月报酬,求
件时,方案二的月报酬不低于方案一的月报酬,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于
的图象相交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.

(1)求一次函数和反比例函数的表达式;
(2)求![]() 的面积;
的面积;
(3)![]() 是
是![]() 轴上一点,且
轴上一点,且![]() 是等腰三角形,请直接写出所有符合条件的
是等腰三角形,请直接写出所有符合条件的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 均为等腰三角形,且
均为等腰三角形,且![]() ,连接
,连接![]() ,
,![]() ,两条线段所在的直线交于点
,两条线段所在的直线交于点![]() .
.

(1)线段![]() 与
与![]() 有何数量关系和位置关系,请说明理由.
有何数量关系和位置关系,请说明理由.
(2)若已知![]() ,
,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,
顺时针旋转,
①如图2,当点![]() 恰好落在
恰好落在![]() 的延长线上时,求
的延长线上时,求![]() 的长;
的长;
②在旋转一周的过程中,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最值.
的最值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+c的顶点(0,5),且过点(﹣3,![]() ),先求抛物线的解析式,再解决下列问题:
),先求抛物线的解析式,再解决下列问题:
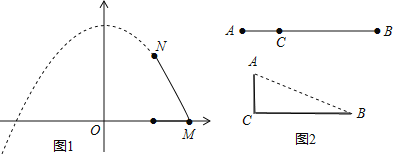
(应用)问题1,如图2,线段AB=d(定值),将其弯折成互相垂直的两段AC、CB后,设A、B两点的距离为x,由A、B、C三点组成图形面积为S,且S与x的函数关系如图所示(抛物线y=ax2+bx+c上MN之间的部分,M在x轴上):
(1)填空:线段AB的长度d= ;弯折后A、B两点的距离x的取值范围是 ;若S=3,则是否存在点C,将AB分成两段(填“能”或“不能”) ;若面积S=1.5时,点C将线段AB分成两段的长分别是 ;
(2)填空:在如图1中,以原点O为圆心,A、B两点的距离x为半径的⊙O;画出点C分AB所得两段AC与CB的函数图象(线段);设圆心O到该函数图象的距离为h,则h= ,该函数图象与⊙O的位置关系是 .
(提升)问题2,一个直角三角形斜边长为c(定值),设其面积为S,周长为x,证明S是x的二次函数,求该函数关系式,并求x的取值范围和相应S的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com