【题目】在数学活动课中，同学们准备了一些等腰直角三角形纸片，从每张纸片中剪出一个扇形制作圆锥玩具模型．如图，已知△ABC是腰长为4的等腰直角三角形．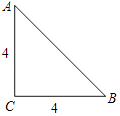 
（1）在等腰直角三角形ABC纸片中，以C为圆心，剪出一个面积最大的扇形（要求：尺规作图，保留作图痕迹，不写作法）；
（2）请求出所制作圆锥底面的半径长．
【答案】
（1）解：如图所示：扇形CEF为所求作的图形；
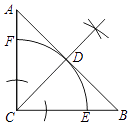
（2）解：∵△ABC是等腰直角三角形，且AC=BC=4，
∴AB= 
，
由（1）可知CD平分∠ACB，
∴CD⊥AB，
∴CD= 
，
设圆锥底面的半径长为r，依题意得：2πr= 
，
∴r= 
，
答：所制作圆锥底面的半径长为
【解析】（1）根据题意作出图形即可；（2根据勾股定理得到AB= ，由（1）可知CD平分∠ACB，根据等腰三角形的性质得到CD⊥AB，根据弧长的公式即可得到结论．
【考点精析】认真审题，首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°)，还要掌握扇形面积计算公式(在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）)的相关知识才是答题的关键．
黄冈经典趣味课堂系列答案
启东小题作业本系列答案科目：初中数学 来源： 题型：
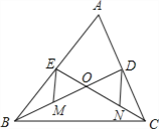
【题目】如图，已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点．
（1）求证：MD和NE互相平分；
（2）若BD⊥AC，EM=2
，OD+CD=7，求△OCB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
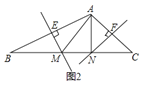
【题目】
如图
所示，在
中，
的垂直平分线交
于点
，交于点
．
的垂直平分线交于点
，交于点
，连接
、
，求证：
的周长
；21.
如图所示，在中，若
，
，的垂直平分线交于点，交于点．的垂直平分线交于点，交于点，连接、，试判断的形状，并证明你的结论．
如图
所示，在中，若
，的垂直平分线交于点，交于点，的垂直平分线交于点，交于点，连接、，若
，
，求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某汽车专买店销售A，B两种型号的新能源汽车，上周售出1辆A型车和3辆B型车，销售额为96万元；本周已售出2辆A型车和1辆B型车，销售额为62万元．
（1）求每辆A型车和B型车的件价各为多少万元；
每辆A型车和B型车的售价分别是x万元，y万元．
根据题意，列方程组
解这个方程组，得x= ，y=
答： ．
（2）有一家公司拟向该店购买A，B两种型号的新能源汽车共6辆，购车费不超过130万元，求这次购进B型车最多几辆？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简
÷（
－
）,然后再从－2＜x≤2的范围内选取一个合适的x的整数值代入求值
【答案】4.
【解析】试题分析：先将原分式进行化解，化解过程中注意不为0的量，根据不为0的量结合x的取值范围得出合适的x的值，将其代入化简后的代数式中即可得出结论．
试题解析：原式=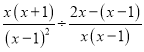
=
=
．
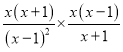其中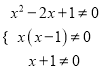
，即x≠﹣1、0、1．
又∵﹣2＜x≤2且x为整数，∴x=2．
将x=2代入
中得： 
=
=4．
考点：分式的化简求值．
【题型】解答题
【结束】
21
【题目】解方程：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，A（﹣2，0），C（2，2），过C作CB⊥x轴于B．
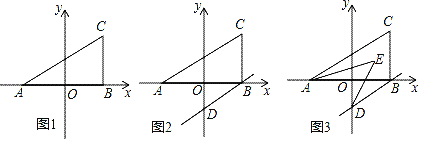
（1）如图1，△ABC的面积是 ；
（2）如图1，在y轴上找一点P，使得△ABP的面积与△ABC的面积相等，请直接写出P点坐标： ；
（3）如图2，若过B作BD∥AC交y轴于D，则∠BAC+∠ODB的度数为 度；
（4）如图3，BD∥AC，若AE、DE分别平分∠CAB，∠ODB，求∠AED的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
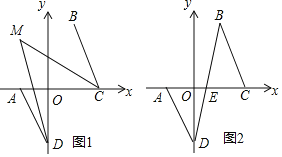
【题目】在直角坐标系中，已知点
，
，
，a是
的立方根，方程
是关于x，y的二元一次方程，d为不等式组
的最大整数解．
求点A、B、C的坐标；
如图1，若D为y轴负半轴上的一个动点，当
时，
与
的平分线交于M点，求
的度数；
如图2，若D为y轴负半轴上的一个动点，连BD交x轴于点E，问是否存在点D，使
？若存在，请求出D的纵坐标
的取值范围；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
