
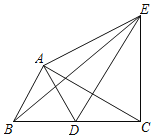
【题目】如图,将两个全等的直角三角尺ABC和ADE如图摆放,∠CAB=∠DAE=90°,∠ACB=∠DEA=30°,使点D落在BC边上,连结EB,EC,则下列结论:①∠DAC=∠DCA;②ED为AC的垂直平分线;③EB平分∠AED;④△ACE为等边三角形.其中正确的是( )
A.①②③B.①②④C.②③④D.①②③④
【答案】B
【解析】
先利用旋转的性质得到AB=AC,AC=AE,则可判断△ABD为等边三角形,所以∠BAD=∠ADB=60°,则∠EAC=∠BAD=60°,再计算出∠DAC=30°,于是可对①进行判断;接着证明△AEC为等边三角形得到EA=EC,得出④正确,加上DA=DC,则根据线段垂直平分线的判定方法可对②进行判断;然后根据平行线和等腰三角形的性质,则可对③进行判断;即可得出结论.
解:在Rt△ABC中,∵∠ACB=30°,
∴∠ABC=60°,
∵△ABC≌△ADE,
∴AB=AD,AC=AE,
∴△ABD为等边三角形,
∴∠BAD=∠ADB=60°,
∵∠CAB=∠DAE=90°
![]() ,
,
![]()
∴∠EAC=∠BAD=60°,
∵∠BAC=90°,
∴∠DAC=30°=∠ACB,
∴∠DAC=∠DCA,①正确;
∵AC=AE,∠EAC=60°,
∴△ACE为等边三角形,④正确;
∴EA=EC,
而DA=DC,
∴ED为AC的垂直平分线,②正确;
∴DE⊥AC,
∵AB⊥AC,
∴AB∥DE,
∴∠ABE=∠BED,
∵AB≠AE,
∴∠ABE≠∠AEB,
∴∠AEB≠∠BED,
∴EB平分∠AED不正确,故③错误;
故选:B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
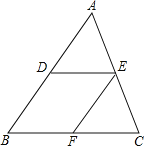
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
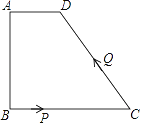
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
(1)求线段CD的长;
(2)t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=BC,以BC为直径的⊙O与AC相交于点D,过点D作DE⊥AB交CB延长线于点E,垂足为点F.
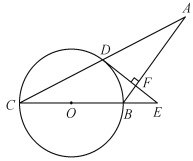
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,且tanC =![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=![]() ;②S△ABC+S△CDE≧S△ACE;③BM⊥DM;④BM=DM,正确结论的个数是( )
;②S△ABC+S△CDE≧S△ACE;③BM⊥DM;④BM=DM,正确结论的个数是( )
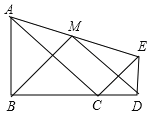
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
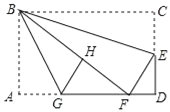
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°; ②△DEF∽△ABG;
③S△ABG=S△FGH; ④AG+DF=FG.
其中正确的是_____.(填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F处,若△FDE的周长为12,△FCB的周长为28,则FC的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com