
【题目】小明在解一元二次方程时,发现有这样一种解法:
如:解方程x(x+4)=6.
解:原方程可变形,得:[(x+2)﹣2][(x+2)+2]=6.
(x+2)2﹣22=6,
(x+2)2=6+22,
(x+2)2=10.
直接开平方并整理,得.x1=﹣2+![]() ,x2=﹣2﹣
,x2=﹣2﹣![]() .
.
我们称小明这种解法为“平均数法”.
(1)下面是小明用“平均数法”解方程(x+3)(x+7)=5时写的解题过程.
解:原方程可变形,得:[(x+a)﹣b][(x+a)+b]=5.
(x+a)2﹣b2=5,
(x+a)2=5+b2.
直接开平方并整理,得.x1=c,x2=d.
上述过程中的a、b、c、d表示的数分别为 , , , .
(2)请用“平均数法”解方程:(x﹣5)(x+3)=6.
【答案】(1)5、2、﹣2、﹣8(2)x1=1+![]() ,x2=1﹣
,x2=1﹣![]()
【解析】(1)、根据阅读材料中的信息确定出上述过程中的“a”,“b”,“c”,“d”表示的数即可;(2)、利用“平均数法”解方程即可.
(1)、原方程可变形,得:[(x+5)﹣2][(x+5)+2]=5.(x+5)2﹣22=5, (x+5)2=5+22.
直接开平方并整理,得.x1=﹣2,x2=﹣8.
上述过程中的a、b、c、d表示的数分别为5、2、﹣2、﹣8,
(2)、原方程可变形,得:[(x﹣1)﹣4][(x﹣1)+4]=6. (x﹣1)2﹣42=6,
(x﹣1)2=6+42. x﹣1=±![]() , ∴x=1±
, ∴x=1±![]() ,
,
直接开平方并整理,得.x1=1+![]() ,x2=1﹣
,x2=1﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】某大型商业中心开业,为吸引顾客,特在一指定区域放置一批按摩休闲椅,供顾客有偿体验,收费如下图:
(1)若在此按摩椅上连续休息了1小时,需要支付多少元?
(2)某人在该椅上一次性消费18元,那么他在该椅子上最多休息了多久?
(3)张先生到该商场会见一名客人,结果客人告知临时有事,预计4.5小时后才能到来;那么如果张先生要在该休闲椅上休息直至客人到来,他至少需要支付多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用的时间为![]() (分),所走的路程为
(分),所走的路程为![]() (米),
(米),![]() 与
与![]() 之间的函数关系如图所示,
之间的函数关系如图所示,
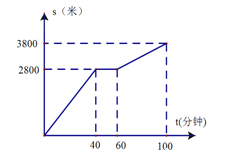
(1)小明中途休息用了_______分钟.
(2)小明在上述过程中所走的过程为________米
(3)小明休息前爬山的平均速度和休息后爬山的平均速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图形是由边长为l的正方形按照某种规律排列而组成的.
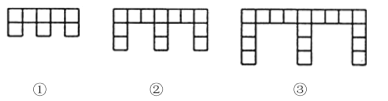
(1)观察图形,填写下表:

(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业在“蜀南竹海”收购毛竹,直接销售,每吨可获利100元,进行粗加工,每天可加工8吨,每吨可获利800元;如果对毛竹进行精加工,每天可加工1吨,每吨可获利4000元.由于受条件限制,每天只能采用一种方式加工,要求将在一月内(30天)将这批毛竹93吨全部销售.为此企业厂长召集职工开会,让职工讨论如何加工销售更合算.
甲说:将毛竹全部进行粗加工后销售;
乙说:30天都进行精加工,未加工的毛竹直接销售;
丙说:30天中可用几天粗加工,再用几天精加工后销售;
请问厂长应采用哪位说的方案做,获利最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为10,
表示的数为10,![]() 是数轴上位于点
是数轴上位于点![]() 左侧一点,且
左侧一点,且![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为
出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() 秒.
秒.
(1)数轴上的点![]() 表示的数是___________,点
表示的数是___________,点![]() 表示的数是__________(用含
表示的数是__________(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点,在点
的中点,在点![]() 运动的过程中,线段
运动的过程中,线段![]() 的长度是__________;
的长度是__________;
(3)动点![]() 从点
从点![]() 处出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点
处出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点![]() 同时发出,问点
同时发出,问点![]() 运动多少秒时与点
运动多少秒时与点![]() 相距4个单位长度?
相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
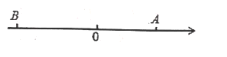
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
![]()
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com