
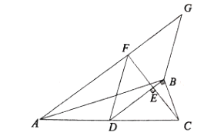
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上的中线,过点
边上的中线,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 的延长线上截取
的延长线上截取![]() ,连接
,连接![]() 、
、![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长为____________.
的长为____________.
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
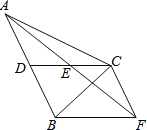
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
(1)求证:CF=AD;
(2)若CA=CB,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
科目:初中数学 来源: 题型:
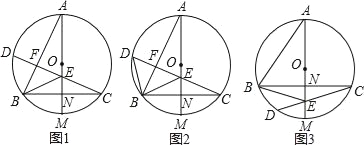
【题目】已知AM是⊙O直径,弦BC⊥AM,垂足为点N,弦CD交AM于点E,连按AB和BE.
(1)如图1,若CD⊥AB,垂足为点F,求证:∠BED=2∠BAM;
(2)如图2,在(1)的条件下,连接BD,若∠ABE=∠BDC,求证:AE=2CN;
(3)如图3,AB=CD,BE:CD=4:7,AE=11,求EM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.

(1)如图1,取点M(1,0),则点M到直线l:y=![]() x﹣1的距离为多少?
x﹣1的距离为多少?
(2)如图2,点P是反比例函数y=![]() 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=
在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=![]() ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
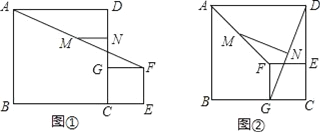
【题目】如图①,C为线段BE上的一点,分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG,M、N分别是线段AF和GD的中点,连接MN
(1)线段MN和GD的数量关系是_____,位置关系是_____;
(2)将图①中的正方形CEFG绕点C逆时针旋转90°,其他条件不变,如图②,(1)的结论是否成立?说明理由;
(3)已知BC=7,CE=3,将图①中的正方形CEFG绕点C旋转一周,其他条件不变,直接写出MN的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com