
【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.(适当添加辅助线,其实并不难)
【答案】解:如图: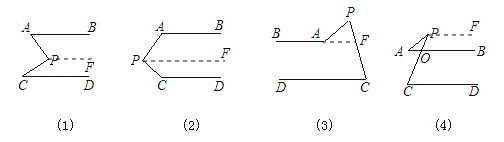
(1)∠APC=∠PAB+∠PCD;
证明:过点P作PF∥AB,则AB∥CD∥PF,
∴∠APC=∠PAB+∠PCD(两直线平行,内错角相等).
(2)∠APC+∠PAB+∠PCD=360°;
(3)∠APC=∠PAB﹣∠PCD;
(4)∵AB∥CD,
∴∠POB=∠PCD,
∵∠POB是△AOP的外角,
∴∠APC+∠PAB=∠POB,
∴∠APC=∠POB﹣∠PAB,
∴∠APC=∠PCD﹣∠PAB.
【解析】关键过转折点作出平行线,根据两直线平行,内错角相等,或结合三角形的外角性质求证即可.
【考点精析】关于本题考查的平行线的性质,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知坐标平面上的机器人接受指令“[a , A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向面对方向沿直线行走a.若机器人的位置在原点,面对方向为y轴的负半轴,则它完成一次指令[2,60°]后,所在位置的坐标为( )
A.(-1, ![]() )
)
B.(-1, ![]() )
)
C.( ![]() ,-1)
,-1)
D.( ![]() ,-1)
,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】火灾猛于虎!据应急管理部统计,2018年全国共接报火灾23.7万起,死亡1407人,伤798人,直接财产损失36.75亿元,其中36.75亿元用科学记数法表示正确的是( )
A. 3.675×109元B. 0.3675×1010元
C. 3.675×108元D. 36.75×108元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线![]() 交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.
交x轴于A、B两点,交y轴于点C,且对称轴为x=﹣2,点P(0,t)是y轴上的一个动点.

(1)求抛物线的解析式及顶点D的坐标.
(2)如图1,当0≤t≤4时,设△PAD的面积为S,求出S与t之间的函数关系式;S是否有最小值?如果有,求出S的最小值和此时t的值.
(3)如图2,当点P运动到使∠PDA=90°时,Rt△ADP与Rt△AOC是否相似?若相似,求出点P的坐标;若不相似,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.(适当添加辅助线,其实并不难)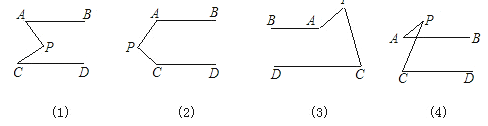
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求:
(1)∠FED的度数;
(2)∠FEG的度数;
(3)∠1和∠2的度数.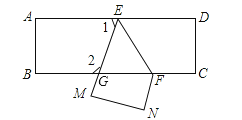
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com