
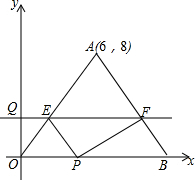
 如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).
如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).分析 (1)过点A作AD⊥OB,由点A的坐标为(6,8),可得OD=6,AD=8,然后由勾股定理得:OA=10,由OA=OB可得:OB=10,进而可得:BD=4,进而可得点B的坐标为:(10,0),然后设OA的关系式:y=kx,然后将A(6,8)代入即可得直线OA的关系式,然后设直线AB的关系式为:y=kx+b,然后将A,B两点代入,即可确定直线AB的关系式,由过点Q作x轴的平行线分别交OA,AB于E,F,可知点Q、E、F三点的纵坐标相等均为t,然后由点E在OA上,点F在AB上,将点E、F的纵坐标分别代入对应的关系式,即可得到得到点E、F的坐标;
(2)由EF∥OP,欲使四边形POEF是平行四边形,只需EF=OP即可,从而可得关于t的等式,解答即可;
(3)分三种情况讨论:①PE⊥EF,②PE⊥PF,③EF⊥PF即可.
解答 解:(1)过点A作AD⊥OB,垂足为D,如图1,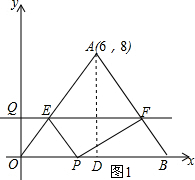
∵点A的坐标为(6,8),
∴OD=6,AD=8,
由勾股定理得:OA=10,
∵OA=OB,
∴OB=10,
∴BD=4,
∴点B的坐标为:(10,0),
设直线OA的关系式:y=kx,
将A(6,8)代入上式,得:
6k=8,
解得:k=$\frac{4}{3}$,
所以直线OA的关系式:y=$\frac{4}{3}$x,
设直线AB的关系式为:y=kx+b,
将A,B两点代入上式得:
$\left\{\begin{array}{l}{6k+b=8①}\\{10k+b=0②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=20}\end{array}\right.$,
所以直线AB的关系式为:y=-2x+20,
∵过点Q作x轴的平行线分别交OA,AB于E,F,
∴点Q、E、F三点的纵坐标相等,
∵动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,
动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,
∴t秒后,OQ=t,OP=2t,
∴Q、E、F三点的纵坐标均为t,
将点E的纵坐标t代入y=$\frac{4}{3}$x,得:x=$\frac{3}{4}$t,
∴E点的坐标为:($\frac{3}{4}t$,t),
将点E的纵坐标t代入y=-2x+20,得:x=10-$\frac{1}{2}$t,
∴F点的坐标为:(10-$\frac{1}{2}$t,t),
故答案为:($\frac{3}{4}$t,t),(10-$\frac{1}{2}$t,t);
(2)由(1)知:E($\frac{3}{4}$t,t),F(10-$\frac{1}{2}$t,t),
∴EF=10-$\frac{1}{2}$t-$\frac{3}{4}$t=10-$\frac{5}{4}$t,
∵四边形POEF是平行四边形,
∴EF∥OP,且EF=OP,
即10-$\frac{5}{4}$t=2t,
解得:t=$\frac{40}{13}$,
∴当t为$\frac{40}{13}$时,四边形POEF是平行四边形;
(3)过点E作EM⊥OB,垂足为M,过点F作FN⊥OB,垂足为N,
可得四边形EMNF是矩形,如图2,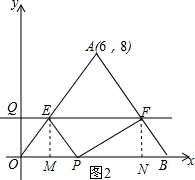
①当PE⊥PF时,PE2+PF2=EF2,
由(1)知:OM=$\frac{3}{4}$t,EM=FN=t,ON=10-$\frac{1}{2}$t,EF=10-$\frac{5}{4}t$,
∴PM=$\frac{5}{4}t$,PN=10-$\frac{5}{2}t$,
∵PE2=ME2+MP2,PF2=PN2+FN2,
∴t2+($\frac{5}{4}$t)2+(10-$\frac{5}{2}$t)2+t2=(10-$\frac{5}{4}t$)2,
解得:t1=0(舍去),t2=$\frac{100}{33}$;
②当PE⊥EF时,如图3,可得四边形EPNF是矩形,
∵四边形EPNF是矩形,
∴EF=PN,
即:EF=ON-OP,
∴10-$\frac{5}{4}t$=10-$\frac{1}{2}t$-2t,
解得t=0(舍去);
③当EF⊥PF时,如图4,可得四边形EMPF是矩形,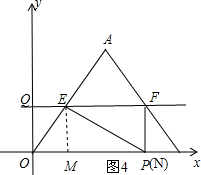
∵四边形EMPF是矩形,
∴EF=MP,
即EF=OP-OM,
∴10-$\frac{5}{4}t$=2t-$\frac{3}{4}$t,
解得:t=4,
∴当t=$\frac{100}{33}$和4时,使△PEF为直角三角形.
点评 此题是一次函数的综合题型,主要考查了用待定系数求一次函数的关系式,点的坐标的确定,动点问题,平行四边形的判定,勾股定理的应用及矩形的性质等知识点,解决第(3)的关键是:分三种情况讨论:①PE⊥EF,②PE⊥PF,③EF⊥PF.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
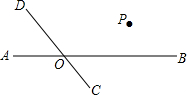 如图,直线CD与直线AB相交于O,根据下列语句画图:
如图,直线CD与直线AB相交于O,根据下列语句画图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
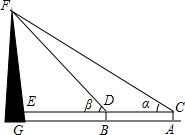 如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).
如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为100cm.
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为100cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
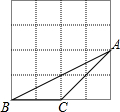 如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )
如图,△ABC的顶点都在边长相等的小正方形的顶点上,则cos∠BAC等于( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com