
| A. | 平均数是1 | B. | 众数是-1 | C. | 中位数是0.5 | D. | 方差是3.5 |
分析 根据众数、中位数、方差和平均数的定义和计算公式分别对每一项进行分析,即可得出答案.
解答 解:这组数据的平均数是:(-1-1+4+2)÷4=1;
-1出现了2次,出现的次数最多,则众数是-1;
把这组数据从小到大排列为:-1,-1,2,4,最中间的数是第2、3个数的平均数,则中位数是$\frac{-1+2}{2}$=0.5;
这组数据的方差是:$\frac{1}{4}$[(-1-1)2+(-1-1)2+(4-1)2+(2-1)2]=4.5;
则下列结论不正确的是D;
故选D.
点评 本题考查了方差、平均数、众数和中位数,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2];一组数据中出现次数最多的数据叫做众数;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
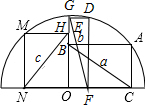 如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
如图,点A、D、G、M在半圆上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )| A. | a>b>c | B. | c>a>b | C. | a=b=c | D. | b>c>a |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的纵坐标为$\frac{3}{2}$.
如图,在平面直角坐标系中,将长方形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(5,4),则点E的纵坐标为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
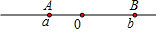 如图所示,数轴上A、B两点分别表示有理数a、b,若c<0,则下列各式:
如图所示,数轴上A、B两点分别表示有理数a、b,若c<0,则下列各式:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com