
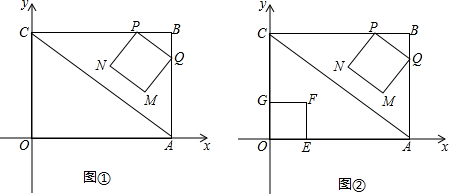
���� ��1����NH��BC�ڵ�H�����ݡ�BPQ�ס�BCA���������������εĶ�Ӧ�ߵı�������BQ��Ȼ��֤����BPQ�ա�HNP����BH�Լ�HN�ij���������t��ʾ����N�����꼴����⣻
��2���������MN��AC��ʱt��ֵ��Ȼ�����������������ۣ����þ��ε������ʽ������⣻
��3�����AC�Ľ���ʽ��Ȼ�����PQ��AC��MN��AC�������PQ��MN�Ľ���ʽ��F�������ǣ�2t��1������F������ֱ����PQ��MN�Ľ���ʽ������⣮
��� 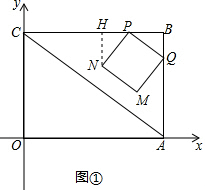 �⣺��1����NH��BC�ڵ�H��
�⣺��1����NH��BC�ڵ�H��
��PQ��CA��
���BPQ�ס�BCA��
��$\frac{BP}{BC}=\frac{BQ}{AB}$����$\frac{2t}{4}=\frac{BQ}{3}$��
��ã�BQ=$\frac{3}{2}$t��
���ڡ�BPQ�͡�HNP��
��$\left\{\begin{array}{l}{��B=��NHP}\\{��HPN=��BQP}\\{PN=QP}\end{array}\right.$��
���BPQ�ա�HNP��
��HP=BQ=$\frac{3}{2}$t��NH=BP=2t��
��BH=2t+$\frac{3}{2}t$=$\frac{7}{2}t$��
��N�����꣨4-$\frac{7}{2}$t��3-2t����
��2����MN��AC��ʱ����ͼ�ڣ�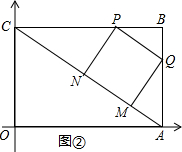
�ߡ�BPQ�ס�BCA��
��$\frac{BP}{BC}=\frac{PQ}{AC}$����$\frac{2t}{4}=\frac{PQ}{5}$��
��ã�PQ=$\frac{5}{2}$t��
��MN��AC��ʱ��PN=PQ=$\frac{5}{2}t$��
��ABC�ס�PNC����$\frac{PN}{AB}=\frac{CP}{AC}$����$\frac{\frac{5}{2}t}{3}=\frac{4-2t}{5}$��
��ã�t=$\frac{24}{37}$��
��S=$\frac{25}{4}$t2��
����0��t��$\frac{24}{37}$��
��t��$\frac{24}{37}$ʱ����PN��AC�ڵ�E����ͼ�ۣ�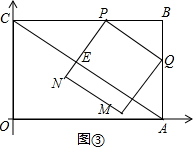
���ABC�ס�PEC����$\frac{PE}{AB}=\frac{CP}{AC}$����$\frac{PE}{3}=\frac{4-2t}{5}$����ã�PE=$\frac{12-6t}{5}$��
��S=-3t2+6t��
����$\frac{24}{37}$��t��2��
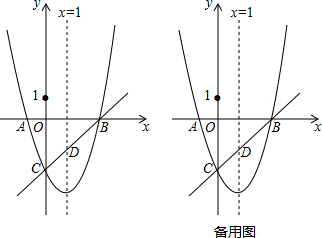
��3����AC�Ľ���ʽ��y=kx+b��
��$\left\{\begin{array}{l}{b=3}\\{4k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=3}\\{k=-\frac{3}{4}}\end{array}\right.$��
����ֱ��MN�Ľ���ʽ��y=-$\frac{3}{4}$x++c��
��-$\frac{3}{4}$��4-$\frac{7}{2}$t��+c=3-2t��
��ã�c=6-$\frac{37}{8}$t��
��ֱ�ߵĽ���ʽ��y=-$\frac{3}{4}$x+��6-$\frac{37}{8}$t����
ͬ����ֱ��PQ�Ľ���ʽ��y=-$\frac{3}{4}$x+��$\frac{25}{3}$-$\frac{8}{3}$t����
F�������ǣ�2t��1����
����F����MN��ʱ��
t=$\frac{40}{49}$��
����F����PQ��ʱ��
��t=$\frac{5}{3}$��
��$\frac{40}{49}$��t��$\frac{5}{3}$��
���� ���⿼�������������ε��ж������ʣ��Լ�ȫ�������ε��к����ʣ���ȷ���MN��AC��ʱ��Ӧ��t��ֵ�ǹؼ���


 Сѧ��ĩ���Ծ�ϵ�д�
Сѧ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪��1=60�㣬���CD��BE����ô��B�Ķ���Ϊ��������
��ͼ����֪��1=60�㣬���CD��BE����ô��B�Ķ���Ϊ��������| A�� | 60�� | B�� | 100�� | C�� | 110 | D�� | 120�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
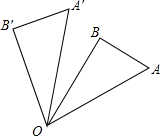 ��ͼ����ֱ�ǡ�OAB�У���AOB=30�㣬OA=2������OAB�Ƶ�O��ʱ����תn��õ���OA��B�䣬���A��OB��OA���С�ֱ�Ϊ��������
��ͼ����ֱ�ǡ�OAB�У���AOB=30�㣬OA=2������OAB�Ƶ�O��ʱ����תn��õ���OA��B�䣬���A��OB��OA���С�ֱ�Ϊ��������| A�� | n�㣬1 | B�� | n�㣬2 | C�� | n��-30�㣬1 | D�� | n��-30�㣬2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
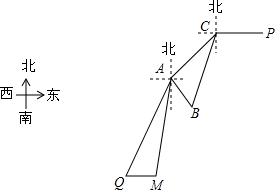 ��ɳȺ���Թ����������й���������ͼ����A��B��C�ֱ��ʾ��ɳȺ��������С������C�ڵ�A�ı�ƫ��45�㷽��B�ڵ�C����ƫ��15�㷽���ϣ���B�ڵ�A����ƫ��30�㷽���ҵ�A����B�����ľ���Ϊ3���
��ɳȺ���Թ����������й���������ͼ����A��B��C�ֱ��ʾ��ɳȺ��������С������C�ڵ�A�ı�ƫ��45�㷽��B�ڵ�C����ƫ��15�㷽���ϣ���B�ڵ�A����ƫ��30�㷽���ҵ�A����B�����ľ���Ϊ3����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
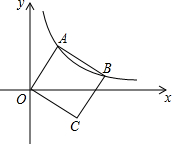 ��ͼ��������OABC��������A��Bǡ���ڷ���������y=$\frac{k}{x}$��k��0��x��0��ͼ���ϣ���֪��A����Ϊ��a��b����
��ͼ��������OABC��������A��Bǡ���ڷ���������y=$\frac{k}{x}$��k��0��x��0��ͼ���ϣ���֪��A����Ϊ��a��b�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com