练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．在△ABC中，若a=$\sqrt{2n}$，b=$\sqrt{{n}^{2}+1}$，c=n-1，则△ABC的形状是（　　）
    A．锐角三角形B．钝角三角形C．等腰三角形D．直角三角形

    分析 根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个是直角三角形判定则可．如果有这种关系，这个就是直角三角形．

    解答 解：∵（n-1）2+（$\sqrt{2n}$）2=（$\sqrt{{n}^{2}+1}$）2，
    ∴三角形为直角三角形．
    故选D．

    点评 本题利用了勾股定理的逆定理判定直角三角形，即已知△ABC的三边满足a2+b2=c2，则△ABC是直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．如图1，点E为正方形ABCD的边AB上一点，EF⊥EC，且EF=EC，连接AF．
    （1）求∠EAF的度数；
    （2）如图2，连接FC交BD于M，交AD于N，求证：$\sqrt{2}$AD=AF+2DM．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．绝对值方程|||x-3.5|-2.5|-1.5|=0.5有8个实数解，该方程的所有解的和是28．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如表是某校七～九年级某月课外兴趣小组（分文艺小组和科技小组）活动时间统计表，其中各年级同一兴趣小组每次活动时间相同．
    课外小组活动总时间h文艺小组活动次数科技小组活动次数
    七年级12.543
    八年级10.533
    九年级7ab
    （Ⅰ）请你完成以下的分析，求出a，b的值：
    观察表格，七、八年级科技小组活动次数相同，文艺小组活动次数相差1次，活动总时间相差2h，由此可知文艺小组每次活动时间为2h，进而可知科技小组每次活动时间为1.5h；
    依题意可得a与b的关系式为2a+1.5b=7，因为a与b是自然数，所以a=2，b=2；
    （Ⅱ）若学校重新规定：九年级每月课外兴趣小组活动总次数为8次，在文艺小组与科技小组每次活动时间保持不变的情况下，求出九年级每月课外兴趣小组活动总时间y（h）与文艺小组活动次数x（次）之间的函数关系式（其中规定x为大于1且小于8的自然数）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．|2-$\sqrt{6}}$|-$\sqrt{{{（3-\sqrt{6}）}^2}}$+$\sqrt{81}$+$\root{3}{-27}$+$\sqrt{（-\frac{2}{3}}{）^2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知点P（x0，y0）和直线y=kx+b，则点P到直线y=kx+b的距离d可用公式d=$\frac{|k{x}_{0}-{y}_{0}+b|}{\sqrt{1+{k}^{2}}}$计算．
    例如：求点P（-1，2）到直线y=3x+7的距离．
    解：因为直线y=3x+7，其中k=3，b=7．
    所以点P（-1，2）到直线y=3x+7的距离为：
    d=$\frac{|k{x}_{0}-{y}_{0}+b|}{\sqrt{1+{k}^{2}}}$=$\frac{|3×（-1）-2+7|}{\sqrt{1+{3}^{2}}}$=$\frac{2}{\sqrt{10}}$=$\frac{\sqrt{10}}{5}$．
    根据以上材料，解答下列问题：
    （1）求点P（1，-1）到直线y=x-1的距离；
    （2）已知⊙Q的圆心Q坐标为（0，5），半径r为2，判断⊙Q与直线y=$\sqrt{3}$x+9的位置关系并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知抛物线C：y1=a（x-h）2-1，直线l：y2=kx-kh-1．
    （1）求证：直线l恒过抛物线C的顶点；
    （2）当a=1，2≤x≤m时，y1≤x-3恒成立，求m的最大值；
    （3）当0＜a≤1，k＞0时，若在直线l下方的抛物线C上至少存在三个横坐标为整数的点，求k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图是某建筑物的屋顶架，其中AB=8m，D是AB的中点，BC，DE都垂直于AC．如果∠ABC=60°，那么BC，DE，CD各是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

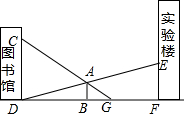    4．某中学的图书馆与实验楼中间有一地标牌AB，小鸣和小夕两位同学分别在图书馆和实验楼的C、E两点处观测地标牌的顶端A，他们的视线如图所示，小鸣从点C处可以看到地面上距离实验楼底部10米远的点G处，小夕从点E恰好可以看到图书馆的底部D处，已知图中的所有点均在同一平面内，CD⊥DF，AB⊥DF，EF⊥DF，CD=6米，EF=3米，DF=25米，请你根据以上数据，求该地标牌的高度AB及它与图书馆之间的距离BD（结果精确到0.1米）．

    查看答案和解析>>

    同步练习册答案