
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЁбCЕФАыОЖЮЊrЃЌИјГіШчЯТЖЈвхЃКШєЕуPЕФКсЁЂзнзјБъОљЮЊећЪ§ЃЌЧвЕНдВаФCЕФОрРыdЁмrЃЌдђГЦPЮЊЁбC ЕФЙиСЊећЕу.
ЃЈ1ЃЉЕБЁбOЕФАыОЖr=2ЪБЃЌдкЕуDЃЈ2ЃЌ-2ЃЉЃЌEЃЈ-1ЃЌ0ЃЉЃЌFЃЈ0ЃЌ2ЃЉжаЃЌЮЊЁбOЕФЙиСЊећЕуЕФЪЧ ЃЛ
ЃЈ2ЃЉШєжБЯп![]() ЩЯДцдкЁбOЕФЙиСЊећЕуЃЌЧвВЛГЌЙ§7ИіЃЌЧѓrЕФШЁжЕЗЖЮЇЃЛ
ЩЯДцдкЁбOЕФЙиСЊећЕуЃЌЧвВЛГЌЙ§7ИіЃЌЧѓrЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЁбCЕФдВаФдкxжсЩЯЃЌАыОЖЮЊ2ЃЌШєжБЯп![]() ЩЯДцдкЁбCЕФЙиСЊећЕуЃЌЧѓдВаФCЕФКсзјБъtЕФШЁжЕЗЖЮЇ.
ЩЯДцдкЁбCЕФЙиСЊећЕуЃЌЧѓдВаФCЕФКсзјБъtЕФШЁжЕЗЖЮЇ.

ЁОД№АИЁПЃЈ1ЃЉEЁЂF ЃЛЃЈ2ЃЉ![]() Ём r ЃМ
Ём r ЃМ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЁмtЁм
ЁмtЁм![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЙиСЊећЕуЕФЖЈвхНјааХаЖЯМДПЩ.
ЃЈ2ЃЉЪзЯШЧѓГіжБЯп![]() ЩЯгавЛИіЁбOЕФЙиСЊећЕуЪБЃЌМДЁбOЙ§ЕуGЃЈ2,2ЃЉЪБЃЌАыОЖrЕФжЕЃЌдйЧѓГіжБЯп
ЩЯгавЛИіЁбOЕФЙиСЊећЕуЪБЃЌМДЁбOЙ§ЕуGЃЈ2,2ЃЉЪБЃЌАыОЖrЕФжЕЃЌдйЧѓГіжБЯп![]() ЩЯга9ИіЁбOЕФЙиСЊећЕуЪБЃЌМДЁбOЙ§ЕуLЃЈ-2,6ЃЉЪБЃЌАыОЖrЕФжЕЃЌМДПЩЧѓНт.
ЩЯга9ИіЁбOЕФЙиСЊећЕуЪБЃЌМДЁбOЙ§ЕуLЃЈ-2,6ЃЉЪБЃЌАыОЖrЕФжЕЃЌМДПЩЧѓНт.
ЃЈ3ЃЉЗжБ№ЧѓГіЕБЁбCЙ§ЕуMЃЈ3,1ЃЉКЭЁбCЙ§ЕуNЃЈ5,-1ЃЉЪБЃЌдВаФCЕФКсзјБъМДПЩ.
ЃЈ1ЃЉЕуD,E,FЕФКсЁЂзнзјБъОљЮЊећЪ§ЃЌЕуDЕНдВаФ![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ВЛТњзуЙиСЊећЕуЕФЖЈвх.
ВЛТњзуЙиСЊећЕуЕФЖЈвх.
ЕуEЕНдВаФ![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ТњзуЙиСЊећЕуЕФЖЈвх.
ТњзуЙиСЊећЕуЕФЖЈвх.
ЕуFЕНдВаФ![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ТњзуЙиСЊећЕуЕФЖЈвх.
ТњзуЙиСЊећЕуЕФЖЈвх.
дђE,FЮЊЁбOЕФЙиСЊећЕу
ЙЪД№АИЮЊЃКEЁЂF ЃЛ
ЃЈ2ЃЉЕБЁбOЙ§ЕуGЃЈ2,2ЃЉЪБЃЌr=![]() ЃЌ
ЃЌ
ЁбOЙ§ЕуLЃЈ-2,6ЃЉЪБЃЌr=![]() ЃЌ
ЃЌ
Ёр![]() Ём r ЃМ
Ём r ЃМ![]()
ЃЈ3ЃЉШчЭМЫљЪОЃК
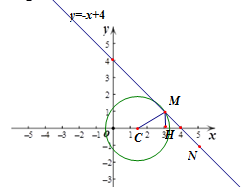
ЕБЁбCЙ§ЕуMЃЈ3,1ЃЉЪБЃЌCM=2ЃЌMH=1ЃЌ
дђCH=![]() ЃЌДЫЪБЕуCЕФКсзјБъt=
ЃЌДЫЪБЕуCЕФКсзјБъt=![]() ЃЌ
ЃЌ
ЕБЁбCЙ§ЕуNЃЈ5,-1ЃЉЪБЃЌЕуCЕФКсзјБъt=![]() ЃЌ
ЃЌ
Ёр![]() ЁмtЁм
ЁмtЁм![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
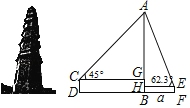
ЁОЬтФПЁПДШЪЯЫўЮЛгкдРбєЪаГЧЮїЖДЭЅКўБпЃЌЪЧКўФЯЪЁБЃДцзюКУЕФЙХЫўНЈжўжЎвЛ.ШчЭМЃЌаЁССЕФФПИпCDЮЊ1.7УзЃЌЫћеОдкDДІВтЕУЫўЖЅЕФбіНЧЁЯACGЮЊ45ЁуЃЌаЁЧйЕФФПИпEFЮЊ1.5УзЃЌЫ§еОдкОрРыЫўЕзжааФBЕуaУздЖЕФFДІЃЌВтЕУЫўЖЅЕФбіНЧЁЯAEHЮЊ62.3Ёу.(ЕуDЁЂBЁЂFдкЭЌвЛЫЎЦНЯпЩЯЃЌВЮПМЪ§ОнЃКsin62.3ЁуЁж0.89ЃЌcos62.3ЁуЁж0.46ЃЌtan62.3ЁуЁж1.9)
(1)ЧѓаЁССгыЫўЕзжааФЕФОрРыBDЃЛ(гУКЌaЕФЪНзгБэЪО)
(2)ШєаЁССгыаЁЧйЯрОр52УзЃЌЧѓДШЪЯЫўЕФИпЖШAB.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНx2+bx+cЃЈbЃЌcЮЊГЃЪ§ЃЉЃЎ
ЃЈЂёЃЉЕБbЃН2ЃЌcЃНЉ3ЪБЃЌЧѓЖўДЮКЏЪ§ЕФзюаЁжЕЃЛ
ЃЈЂђЃЉЕБcЃН5ЪБЃЌШєдкКЏЪ§жЕyЃН1ЕФЧщПіЯТЃЌжЛгавЛИіздБфСПxЕФжЕгыЦфЖдгІЃЌЧѓДЫЪБЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈЂѓЃЉЕБcЃН5ЪБЃЌдкздБфСПxЕФжЕТњзу1ЁмxЁм3ЕФЧщПіЯТЃЌгыЦфЖдгІЕФКЏЪ§жЕyЕФзюаЁжЕЮЊЉ5ЃЌЧѓbЕФжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЙигкЖўДЮКЏЪ§ЕФЫЕЗЈДэЮѓЕФЪЧ( )
A.ЖўДЮКЏЪ§y=(x+2)2Ѓ2ЕФЖЅЕузјБъЪЧ(Ѓ2,Ѓ2)
B.ХзЮяЯпy=Ѓx2 +2x+1ЃЌЕБx<0ЪБyЫцxЕФдіДѓЖјдіДѓ
C.КЏЪ§y= 2x2 + 4xЃ3ЕФЭМЯѓЕФзюЕЭЕузјБъЮЊ(Ѓ1,Ѓ5)
D.ЕуA(3,0)ВЛдкХзЮяЯпy=x2Ѓ2xЃ3ЕФЭМЯѓЩЯ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЬхг§ВтЪдЪБЃЌОХФъМЖвЛУћФаЩњЃЌЫЋЪжШгЪЕаФЧђЃЌвбжЊЪЕаФЧђЫљОЙ§ЕФТЗЯпЪЧФГИіЖўДЮКЏЪ§ЭМЯѓЕФвЛВПЗжЃЌШчЙћЧђГіЪжДІAЕуОрРыЕиУцЕФИпЖШЮЊ2mЃЌЕБЧђдЫааЕФЫЎЦНОрРыЮЊ6mЪБЃЌДяЕНзюДѓИпЖШ5mЕФBДІЃЈШчЭМЃЉЃЌЮЪИУФаЩњАбЪЕаФЧђШгГіЖрдЖЃПЃЈНсЙћБЃСєИљКХЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНЉx2+2x+3ЃЎ
ЃЈ1ЃЉЧѓЫќЕФЖдГЦжсКЭЖЅЕузјБъЃЛ
ЃЈ2ЃЉЧѓИУХзЮяЯпгыxжсЕФНЛЕузјБъЃЛ
ЃЈ3ЃЉНЈСЂЦНУцжБНЧзјБъЯЕЃЌЛГіетЬѕХзЮяЯпЕФЭМЯѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНЉx2+2x+3ЃЎ
ЃЈ1ЃЉЧѓЫќЕФЖдГЦжсКЭЖЅЕузјБъЃЛ
ЃЈ2ЃЉЧѓИУХзЮяЯпгыxжсЕФНЛЕузјБъЃЛ
ЃЈ3ЃЉНЈСЂЦНУцжБНЧзјБъЯЕЃЌЛГіетЬѕХзЮяЯпЕФЭМЯѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋЁїABCШЦЕуAЫГЪБеыа§зЊ60ЁуЕУЕНЁїADEЃЌЕуCЕФЖдгІЕуEЧЁКУТфдкBAЕФбгГЄЯпЩЯЃЌDEгыBCНЛгкЕуFЃЌСЌНгBDЃЎЯТСаНсТлВЛвЛЖЈе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
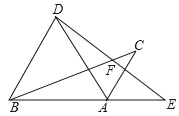
A. AD=BD B. ACЁЮBD C. DF=EF D. ЁЯCBD=ЁЯE
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЯЪРжЁБЫЎЙћЕъЙКНјвЛгХжЪЫЎЙћЃЌНјМлЮЊ 10 дЊ/ЧЇПЫЃЌЪлМлВЛЕЭгк 10 дЊ/ЧЇПЫЃЌЧвВЛГЌЙ§ 16 дЊ/ЧЇПЫЃЌИљОнЯњЪлЧщПіЃЌЗЂЯжИУЫЎЙћвЛЬьЕФЯњЪлСП yЃЈЧЇПЫЃЉ гыИУЬьЕФЪлМл xЃЈдЊ/ЧЇПЫЃЉТњзуШчЯТБэЫљЪОЕФвЛДЮКЏЪ§ЙиЯЕ
ЯњЪлСП yЃЈЧЇПЫЃЉ | Ё | 29 | 28 | 27 | 26 | Ё |
ЪлМл xЃЈдЊ/ЧЇПЫЃЉ | Ё | 10.5 | 11 | 11.5 | 12 |
ЃЈ1ЃЉФГЬьетжжЫЎЙћЕФЪлМлЮЊ 14 дЊ/ЧЇПЫЃЌЧѓЕБЬьИУЫЎЙћЕФЯњЪлСПЃЛ
ЃЈ2ЃЉШчЙћФГЬьЯњЪлетжжЫЎЙћЛёРћ 100 дЊЃЌФЧУДИУЬьЫЎЙћЕФЪлМлЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com