
 如图,点I为△ABC的内心,点O为△ABC的外心,若∠BIC=140°,则∠BOC=160°.
如图,点I为△ABC的内心,点O为△ABC的外心,若∠BIC=140°,则∠BOC=160°. 分析 因为点I为△ABC的内心,推出∠IAB+∠IBA=$\frac{1}{2}$(∠ABC+∠ACB)=180°-140°=40°,推出∠ABC+∠ACB=80°,推出∠A=180°-(∠ABC+∠ACB)=100°,
作△ABC的外接圆如图,在⊙O上取一点D,连接BD、CD.因为∠D=180°-∠A=80°,根据∠BOC=2∠D即可解决问题.
解答 解:∵点I为△ABC的内心,
∴∠IAB+∠IBA=$\frac{1}{2}$(∠ABC+∠ACB)=180°-140°=40°,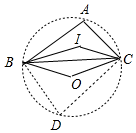
∴∠ABC+∠ACB=80°,
∴∠A=180°-(∠ABC+∠ACB)=100°
∵点O为△ABC的外心,作△ABC的外接圆如图,在⊙O上取一点D,连接BD、CD.
∴∠D=180°-∠A=80°,
∴∠BOC=2∠D=160°.
故答案为160.
点评 此题主要考查了三角形的内心和外心,正确把握三角形内心的性质是解题关键,记住钝角三角形的外心在三角形外,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
 如图.已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于点A(-2,4),B(8,2),根据图象能使y1>y2成立的x取值范围是x<-2或x>8.
如图.已知二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象相交于点A(-2,4),B(8,2),根据图象能使y1>y2成立的x取值范围是x<-2或x>8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在⊙O内接四边形ABCD中,∠ABC=60°,AB=BC=6,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为11$\sqrt{3}$,则△BEF的面积为5$\sqrt{3}$.
如图,在⊙O内接四边形ABCD中,∠ABC=60°,AB=BC=6,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为11$\sqrt{3}$,则△BEF的面积为5$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点E在四边形ABCD的边BC的延长线上,则下列两个角是同位角的是( )
如图,点E在四边形ABCD的边BC的延长线上,则下列两个角是同位角的是( )| A. | ∠BAC和∠ACB | B. | ∠B和∠DCE | C. | ∠B和∠BAD | D. | ∠B和∠ACD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com