
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴分别交于点C,其中点A(﹣1,0),OB=4OA,OC=2OA
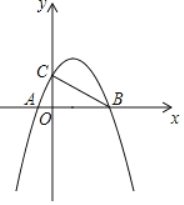
(1)求抛物线的解析式.
(2)点P是线段AB一动点,过P作PD∥AC交BC于D,当△PCD面积最大时,求点P的坐标.
(3)点M是位于线段BC上方的抛物线上一点,当∠ABC恰好等于△BCM中的某个角时,直接写出点M的坐标.
【答案】(1)y=![]() ;(2)P(
;(2)P(![]() ,0);(3)M点的坐标为(3,2)或(
,0);(3)M点的坐标为(3,2)或(![]() )
)
【解析】
(1)先根据B(4,0),C(0,2),设抛物线的解析式为:y=a(x+1)(x﹣4),将点(0,2)代入求出![]() ,然后将原抛物线解析式化为一般式即可;
,然后将原抛物线解析式化为一般式即可;
(2)设P(m,0),则OC=2,AB=5,BP=4-m,然后根据三角形面积公式列出二次函数解析式,利用二次函数的性质求解即可;
(3)分两种情况求解:当∠BCM=∠ABC时和当∠CBM=∠ABC时.
解:(1)由条件可知:B(4,0),C(0,2)
设抛物线的解析式为:y=a(x+1)(x﹣4),将点(0,2)代入上式得:
a×1×(﹣4)=2解得:a=﹣![]() ,
,
∴抛物线的解析式为y=![]() ;
;
(2)如图1,设P(m,0),则OC=2,AB=5,BP=4-m
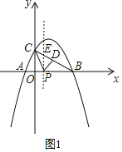
SΔABC=![]() AB×OC=5
AB×OC=5
∵PD//AC∴ΔABC∽ΔPDB
∴![]()
∴![]()
∴![]()
∵SΔPCB=![]() PB×OC=4-m
PB×OC=4-m
∴SΔPCD=SΔPCB-SΔPDB=4-m-![]() =
=![]()
∴当m=![]() 时,ΔPCM面积最大
时,ΔPCM面积最大
∴P(![]() ,0).
,0).
(3)由题意知,∠BMC≠∠ABC,
当∠BCM=∠ABC时,CM∥AB,如图2,
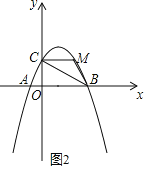
∴点C与点M关于抛物线的对称轴对称,
∴M(3,2);
当∠CBM=∠ABC时,如图3,过M作MF⊥BC于F,过F作y轴的平行线,交x轴于G,交过M平行于x轴的直线于K,
∵∠CBM=∠ABC,∠BFM=∠BGF,
∴△MFK∽△FGB,
同理可证:△MBF∽△MFK∽△FBG∽△CBO,
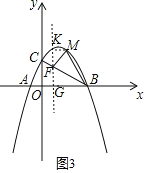
∴![]() ,
,![]() .
.
设G(n,0),则F(n,﹣![]() n+2),
n+2),
∴![]() ,KF=﹣
,KF=﹣![]() n+2,
n+2,
∴M(![]() n+1,-n+4),代入抛物线解析式可解得,
n+1,-n+4),代入抛物线解析式可解得,
n=![]() ,n=4(舍去).
,n=4(舍去).
∴M(![]() ).
).
综合以上可得M点的坐标为(3,2)或(![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,D是![]() 的中点,BC与AD,OD分别交于点E,F.
的中点,BC与AD,OD分别交于点E,F.
(1)求证:OD∥AC;
(2)求证:DC2=DEDA;
(3)若⊙O的直径AB=10,AC=6,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
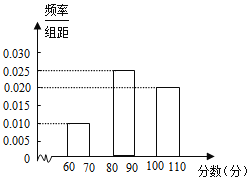
【题目】某社区为了加强居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与作答《2020年新型冠状病毒肺炎的防护全国统一考试(全国卷)》试卷(满分100分),社区管理员随机从该社区抽取40名居民的答卷,并对他们的成绩(单位:分)进行整理、分析,过程如下:
收集数据
85 65 95 100 90 95 85 65 75 85 100 90 70 90 100 80 80 100 95 75 80 100 80 95 65 100 90 95 85 80 100 75 60 90 70 80 95 75 100 90
整理数据(每组数据可含最低值,不含最高值)
分组(分) | 频数 | 频率 |
60~70 | 4 | 0.1 |
70~80 | a | b |
80~90 | 10 | 0.25 |
90~100 | c | d |
100~110 | 8 | 0.2 |
分析数据
(1)填空:a= ,b= ,c= ,d= ;
(2)补全频率分布直方图;
(3)由此估计该社区居民在线答卷成绩在 (分)范围内的人数最多;
(4)如果该社区共有800人参与答卷,那么可估计该社区成绩在90分及以上约为 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中∠A=∠ABC=90°,点E是CD的中点,△ABD与 △EBD关于直线BD对称,![]() ,
,![]() .
.
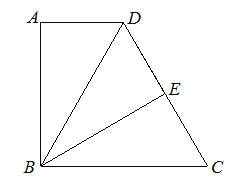
(1)求点A和点E之间的距离;
(2)联结AC交BE于点F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=30°,直线a∥b,顶点C在直线b上,直线a交AB于点D,交AC于点E,若∠1=145°,则∠2的度数是( )
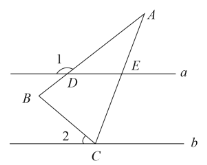
A.30°B.35°C.40°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
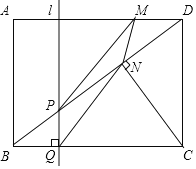
【题目】如图,在矩形ABCD中,CD=3cm,BC=4cm,连接BD,并过点C作CN⊥BD,垂足为N,直线l垂直BC,分别交BD、BC于点P、Q.直线l从AB出发,以每秒1cm的速度沿BC方向匀速运动到CD为止;点M沿线段DA以每秒1cm的速度由点D向点A匀速运动,到点A为止,直线1与点M同时出发,设运动时间为t秒(t>0).
(1)线段CN= ;
(2)连接PM和QN,当四边形MPQN为平行四边形时,求t的值;
(3)在整个运动过程中,当t为何值时△PMN的面积取得最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 内接于
内接于![]() 分别是
分别是![]() 和
和![]() 所对弧的中点,弦
所对弧的中点,弦![]() 分别交
分别交![]() 于点
于点![]() ,连结
,连结![]()
(1)求证:![]() 是等边三角形.
是等边三角形.
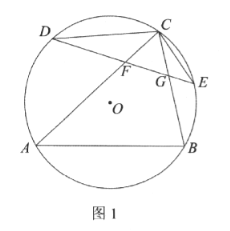
(2)若![]()
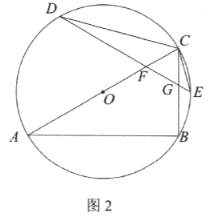
①如图2,当![]() 为
为![]() 的直径时,求
的直径时,求![]() 的长.
的长.
②当![]() 将
将![]() 的面积分成了
的面积分成了![]() 的两部分时,求
的两部分时,求![]() 的长.
的长.
(3)连结![]() 交
交![]() 于点
于点![]() ,若
,若![]() :则
:则![]() 的值为_______. (请直接写出答案)
的值为_______. (请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
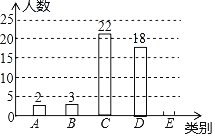
【题目】某校响应国家号召,鼓励学生积极参与体育锻炼.为了解学生一星期参与体育锻炼的时间情况,从全校2000名学生中,随机抽取50名学生进行调查,按参与体育锻炼的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
(1)样本中E类学生有 人,补全条形统计图;
(2)估计全校的D类学生有 人;
(3)从该样本参与体育锻炼时间在0≤t≤4的学生中任选2人,求这2人参与体育锻炼时间都在2<t≤4中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com