

科目:初中数学 来源:不详 题型:解答题
 ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.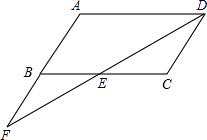
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,∠A=90°;小区为美化环境,欲在空地上铺草坪,已知草坪每平方米150元,试问铺满这块空地共需花费多少元?
,∠A=90°;小区为美化环境,欲在空地上铺草坪,已知草坪每平方米150元,试问铺满这块空地共需花费多少元?
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的面积是多少平方米?
的面积是多少平方米? 做一个纸箱比方案1更优,你认为呢?请说明理由.
做一个纸箱比方案1更优,你认为呢?请说明理由.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com