
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积.
(2)若连接AD、CF,则这两条线段之间的关系是 ;
(3)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP.
科目:初中数学 来源: 题型:
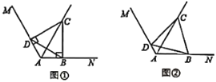
【题目】已知射线AC是∠MAN的角平分线, ∠NAC=60°, B, D分别是射线AN. AM上的点,连接BD.
(1)在图①中,若∠ABC=∠ADC=90°,求∠CDB的大小;
(2)在图②中,若∠ABC+∠ADC=180°,求证:四边形ABCD的面积是个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是![]() 的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下
的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下![]() 型与
型与![]() 型两种板材.如图所示,(单位:
型两种板材.如图所示,(单位:![]() )
)

(1)列出方程(组),求出图甲中![]() 与
与![]() 的值.
的值.
(2)在试生产阶段,若将![]() 张标准板材用裁法一裁剪,
张标准板材用裁法一裁剪,![]() 张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.
张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒![]() 个,横式无盖礼品盒的
个,横式无盖礼品盒的![]() 个,根据题意完成表格:
个,根据题意完成表格:
礼品盒板 材 | 竖式无盖(个) | 横式无盖(个) |
|
| |
A型(张) |
|
|
B型(张) |
|

③做成的竖式和横式两种无盖礼品盒总数最多是 个;
此时,横式无盖礼品盒可以做 个(在横线上直接写出答案,无需书写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为m(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个直角边长为4,面积为6的直角三角形.
(2)画一个底边长为4,面积为8的等腰三角形.
(3)画一个面积为5的等腰直角三角形.
(4)画一个边长为2![]() ,面积为6的等腰三角形.
,面积为6的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处(点C在∠AOB的内部或一边上).
(1)当PC∥QB时,OQ= cm.
(2)当折叠后重叠部分为等腰三角形时,画出示意图,写出OQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s | 150 | 300 | 600 | 900 | 1200 | 1500 |
摸到白球的频数n | 63 | a | 247 | 365 | 484 | 606 |
摸到白球的频率 | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
(1) 按表格数据格式,表中的![]() = ;
= ;![]() = ;
= ;
(2) 请估计:当次数s很大时,摸到白球的频率将会接近 (精确到0.1);
(3)请推算:摸到红球的概率是 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再回答问题:如果x1、x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,那么x1+x2 , x1x2与系数a、b、c的关系是:x1+x2= ![]() ,
, ![]() ,例如:若x1、x2是方程2x2﹣x﹣1=0的两个根,则x1+x2=﹣
,例如:若x1、x2是方程2x2﹣x﹣1=0的两个根,则x1+x2=﹣ ![]() =
= ![]()
![]() ,x1x2=
,x1x2= ![]() .若x1、x2是方程2x2+x﹣3=0的两个根.
.若x1、x2是方程2x2+x﹣3=0的两个根.
(1)求x1+x2 , x1x2;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形;
(2)证明:DE=BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com