
运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.
【小题1】如图1,在等腰三角形ABC中,AB=AC,AC边上的高为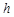 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为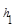 、
、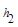 .连接AM,可得结论
.连接AM,可得结论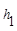 +
+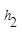 =
=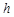 .当点M在BC延长线上时,
.当点M在BC延长线上时,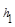 、
、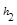 、
、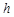 之间的等量关系式是 .(直接写出结论不必证明).
之间的等量关系式是 .(直接写出结论不必证明).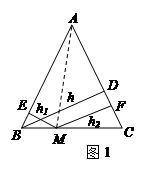
【小题2】应用:平面直角坐标系中有两条直线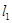 :
: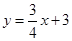 、
、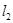 :
: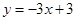 ,若
,若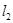 上的一点M到
上的一点M到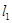 的距离是1.请运用(1)的条件和结论求出点M的坐标.
的距离是1.请运用(1)的条件和结论求出点M的坐标.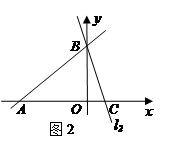
科目:初中数学 来源: 题型:

| 3 |
| 4 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.
1.如图1,在等腰三角形ABC中,AB=AC,AC边上的高为![]() ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为![]() 、
、![]() .连接AM,可得结论
.连接AM,可得结论![]() +
+![]() =
=![]() .当点M在BC延长线上时,
.当点M在BC延长线上时,![]() 、
、![]() 、
、![]() 之间的等量关系式是 .(直接写出结论不必证明).
之间的等量关系式是 .(直接写出结论不必证明).

2.应用:平面直角坐标系中有两条直线![]() :
:![]() 、
、![]() :
:![]() ,若
,若![]() 上的一点M到
上的一点M到![]() 的距离是1.请运用(1)的条件和结论求出点M的坐标.
的距离是1.请运用(1)的条件和结论求出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
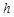 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为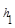 、
、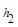 .连接AM,可得结论
.连接AM,可得结论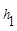 +
+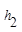 =
=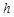 .当点M在BC延长线上时,
.当点M在BC延长线上时,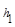 、
、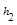 、
、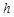 之间的等量关系式是 .(直接写出结论不必证明).
之间的等量关系式是 .(直接写出结论不必证明).
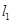 :
: 、
、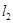 :
: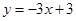 ,若
,若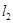 上的一点M到
上的一点M到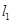 的距离是1.请运用(1)的条件和结论求出点M的坐标.
的距离是1.请运用(1)的条件和结论求出点M的坐标.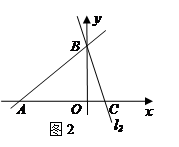
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省盐城市阜宁县羊寨中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
运用“同一图形的面积不同表示方式相同”可以证明一类含有线段的等式,这种解决问题的方法我们称之为面积法.
(1)如图,在等腰三角形ABC中,AB=AC,AC边上的高为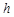 ,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为
,M是底边BC上的任意一点,点M到腰AB、AC的距离分别为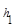 、
、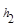 .连接AM,可得结论
.连接AM,可得结论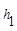 +
+ =
=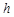 .当点M在BC延长线上时,
.当点M在BC延长线上时, 、
、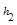 、
、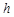 之间的等量关系式是 .(直接写出结论不必证明).
之间的等量关系式是 .(直接写出结论不必证明).
(2)应用:平面直角坐标系中有两条直线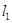 :
: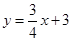 、
、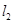 :
: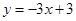 ,若
,若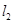 上的一点M到
上的一点M到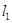 的距离是1.请运用(1)的条件和结论求出点M的坐标.
的距离是1.请运用(1)的条件和结论求出点M的坐标.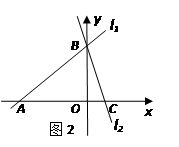

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com