
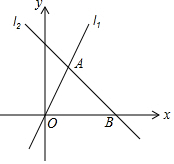
 如图,在平面直角坐标系xOy中,直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(2,4),直线l2与x轴交于点B(6,0).
如图,在平面直角坐标系xOy中,直线l1:y=mx(m≠0)与直线l2:y=ax+b(a≠0)相交于点A(2,4),直线l2与x轴交于点B(6,0).分析 (1)利用待定系数法求直线l1,l2的表达式;
(2)直线在点A的下方时符合条件,根据图象写出结果.
解答 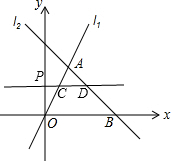 解:(1)∵点A(2,4)在l1:y=mx上,
解:(1)∵点A(2,4)在l1:y=mx上,
∴2m=4,
∴m=2,
∴直线l1的表达式为y=2x,
∵点A(2,4)和B(6,0)在直线l2:y=ax+b上,
∴$\left\{\begin{array}{l}{2a+b=4}\\{6a+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=6}\end{array}\right.$,
∴直线l2的表达式为y=-x+6;
(2)由图象得:当点C位于点D左方时,n的取值范围是:n<4.
点评 本题考查用待定系数法求解函数解析式、两直线平行和相交的问题,明确待定系数法只需把所给的点的坐标代入函数表达式列方程或方程组解出即可,同时利用数形结合的思想求n的取值.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:解答题
 如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠1=∠2=50°.
如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠1=∠2=50°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年龄 | 13 | 14 | 15 | 16 | 17 |
| 人数 | 2 | 1 | 4 | 1 | 2 |
| 年龄 | 3 | 4 | 5 | 6 | 54 | 57 |
| 人数 | 1 | 2 | 2 | 3 | 1 | 1 |
| 平均数 | 中位数 | 众数 | 方差 | |
| 甲队游客年龄 | 15 | 15 | 15 | 1.8 |
| 乙队游客年龄 | 15 | 5.5 | 6 | 11.4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 符合数轴所表示的解集的不等式组是( )
符合数轴所表示的解集的不等式组是( )| A. | $\left\{\begin{array}{l}{x+1>0}\\{4-x>0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1>0}\\{x-4>0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+1<0}\\{x-4>0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+1<0}\\{4-x>0}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E、F是⊙O上两点,连接AE、CF、DF,满足EA=CA.
如图,Rt△ABC中,∠ACB=90°,以BC为直径的⊙O交AB于点D,E、F是⊙O上两点,连接AE、CF、DF,满足EA=CA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com