练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】点A（﹣3，5）关于原点的对称点的坐标为（　　）
    A.（3，5）
    B.（﹣3，﹣5）
    C.（3，﹣5）
    D.（5，﹣3）

    【答案】C
    【解析】解：点A（﹣3，5）关于原点的对称点的坐标为：（3，﹣5）．
    故选：C．
    【考点精析】通过灵活运用关于原点对称的点的坐标，掌握两个点关于原点对称时，它们的坐标的符号相反，即点P（x，y）关于原点的对称点为P’（-x，-y）即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知△ABC与△DEF相似且周长比为2：5，则△ABC与△DEF的相似比为

    查看答案和解析>>

    科目：初中数学 来源： 题型：

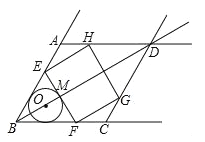
    【题目】(2016浙江省温州市第24题)如图，在射线BA，BC，AD，CD围成的菱形ABCD中，∠ABC=60°，AB=6，O是射线BD上一点，⊙O与BA，BC都相切，与BO的延长线交于点M．过M作EF⊥BD交线段BA（或射线AD）于点E，交线段BC（或射线CD）于点F．以EF为边作矩形EFGH，点G，H分别在围成菱形的另外两条射线上．

    （1）求证：BO=2OM．

    （2）设EF＞HE，当矩形EFGH的面积为24时，求⊙O的半径．

    （3）当HE或HG与⊙O相切时，求出所有满足条件的BO的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC．将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线．此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE．则说明这两个三角形全等的依据是（　　）

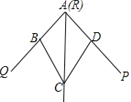
    A. SAS B. ASA C. AAS D. SSS

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(2016贵州省毕节市第25题)阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M（1，3）的特征线有：x=1，y=3，y=x+2，y=﹣x+4．

    问题与探究：如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线经过B、C两点，顶点D在正方形内部．

    （1）直接写出点D（m，n）所有的特征线；

    （2）若点D有一条特征线是y=x+1，求此抛物线的解析式；

    （3）点P是AB边上除点A外的任意一点，连接OP，将△OAP沿着OP折叠，点A落在点A′的位置，当点A′在平行于坐标轴的D点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP上？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知线段AB，延长线段AB到点C，使，且BC比AB大1，D是线段AB的中点，如图所示.

    (1)求线段CD的长；

    (2)线段AC的长是线段DB的几倍?

    (3)线段AD的长是线段BC的几分之几?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

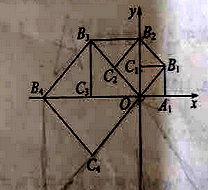
    【题目】(2016山东省聊城市第17题)如图，在平面直角坐标系中，边长为1的正方形OA1B1C1的两边在坐标轴上，以它的对角线OB1为边作正方形OB1B2C2，再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3，以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班有48名同学，在一次英语单词竞赛成绩统计中，成绩在81～ 90这一分数段的人数所占的频率是0.25，那么成绩在这个分数段的同学有_________名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y=（x﹣1）2+2的最小值是（　　）
    A.-2
    B.-1
    C.1
    D.2

    查看答案和解析>>

    同步练习册答案