
【题目】一个不透明的口袋中有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个,小明将球搅匀后从中摸出一个球是红球的概率是0.25.
(1)求口袋中红球的个数;
(2)若小明第一次从中摸出一个球,放回搅匀后再摸出一个球,请通过树状图或者列表的方法求出小明两次均摸出红球的概率.
【答案】(1)口袋中红球有1个;(2)小明两次均摸出红球的概率:P(红,红)=![]() .
.
【解析】
(1)设红球有x个,根据概率公式列出方程,然后求解即可;
(2)根据题意列出图表得出所有等情况数和小明两次均摸出红球的个数,再根据概率公式即可得出答案.
(1)设红球有x个,依题意得:
![]()
解得:x=1,
经检验:x=1是原方程的解
答:口袋中红球有1个.
(2)根据题意列表如下:
白1 | 白2 | 黄 | 红 | |
白1 | (白1,白1) | (白1,白2) | (白1,黄) | (白1,红) |
白2 | (白2,白1) | (白2,白2) | (白2,黄) | (白2,红) |
黄 | (黄,白1) | (黄,白2) | (黄,黄) | (黄,红) |
红 | (红,白1) | (红,白2) | (红,黄) | (红,红) |
共有16种等情况数,其中两次均摸出红球的有1种,
所以小明两次均摸出红球的概率:P(红,红)=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
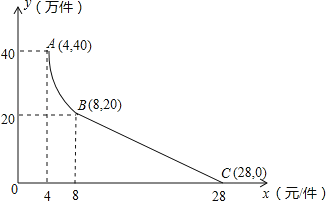
【题目】某公司用100万元研发一种市场急需电子产品,已于当年投入生产并销售,已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,设公司销售这种电子产品的年利润为s(万元).
(1)请求出y(万件)与x(元/件)的函数表达式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)的函数表达式,并求出第一年年利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
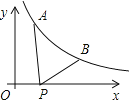
【题目】如图所示,已知A(![]() ,y1),B(2,y2)为反比例函数
,y1),B(2,y2)为反比例函数![]() 图像上的两点,动点P(x,0)在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图像上的两点,动点P(x,0)在x正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A. (![]() ,0) B. (1,0) C. (
,0) B. (1,0) C. (![]() ,0) D. (
,0) D. (![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
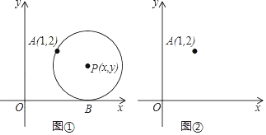
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式;判断此函数图象的形状;并在图②中画出此函数的图象;
(3)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=ax2+bx+c(a>0)的图象与x轴交于A(﹣1,0)、B(n,0)两点,一次函数y2=2x+b的图象过点A.
(1)若a=![]() ,
,
①求二次函数y1=ax2+bx+c(a>0)的函数关系式;
②设y3=y1﹣my2,是否存在正整数m,当x≥0时,y3随x的增大而增大?若存在,求出正整数m的值;若不存在,请说明理由;
(2)若![]() <a<
<a<![]() ,求证:﹣5<n<﹣4.
,求证:﹣5<n<﹣4.
查看答案和解析>>
科目:初中数学 来源: 题型:
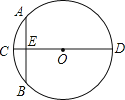
【题目】“圆材埋壁”是我国古代数一学著作《九章算术》中的一个问题.“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表达是:如图所示,CD为⊙O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=1尺,则直径CD长为_____寸.
查看答案和解析>>
科目:初中数学 来源: 题型:
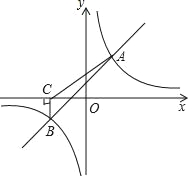
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(2,3),B(﹣3,n)两点.
的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)过点B作BC⊥x轴,垂足为C,连接AC,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“节能减排、绿色出行”的健康生活意识的普及,新能源汽车越来越多地走进百姓的生活.某汽车租赁公司拥有40辆电动汽车,据统计,当每辆车的日租金为120元时,可全部租出;当每辆车的日租金每增加5元时,未租出的车将增加1辆;该公司平均每日的各项支出共2100元.
(1)若某日共有x辆车未租出,则当日每辆车的日租金为 元;
(2)当每辆车的日租金为多少时,该汽车租赁公司日收益最大?最大日收益是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com