
【题目】如图,AB为⊙O的直径,弦CD⊥AB于E,∠CDB=15°,OE=2![]() .
.
(1)求⊙O的半径;
(2)将△OBD绕O点旋转,使弦BD的一个端点与弦AC的一个端点重合,则弦BD与弦AC的夹角为 .

【答案】60°或90°
【解析】试题分析:(1)求出∠BOD的度数,在Rt△ODE中,根据∠DOE=30°,OE=2![]() ,求出DE和OD即可;
,求出DE和OD即可;
(2)分为4种情况,分别求出∠CAB和∠OAB(或∠OAD、∠OCB)的度数,相加(或相减)即可求出答案.
试题解析:(1)∵AB为⊙O的直径,弦CD⊥AB于E,
∴![]() ,
,
∴∠BDC=![]() ∠BOD,
∠BOD,
而∠CDB=15°,
∴∠BOD=2×15°=30°,
在Rt△ODE中,∠DOE=30°,OE=2![]() ,
,
∴OE=![]() DE,OD=2DE,
DE,OD=2DE,
∴DE=![]() =2,
=2,
∴OD=4,
即⊙O的半径为4;
(2)有4种情况:如图:
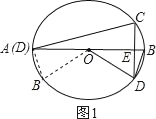



①如图1所示:∵OA=OB,∠AOB=30°,
∴∠OAB=∠OBA=75°,
∵CD⊥AB,AB是直径,
∴弧BC=弧BD,
∴∠CAB=![]() ∠BOD=15°,
∠BOD=15°,
∴∠CAB=∠BAO+∠CAB=15°+75°=90°;
②如图2所示,∠CAD=75°﹣15°=60°;
③如图3所示:∠ACB=90°;
④如图4所示:∠ACB=60°;
故答案为:60°或90°.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】在①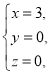 ②
②![]() ③
③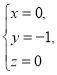 这三对数值中,__________是方程x+2y+z=3的解,__________是方程2x-y-z=1的解,__________是方程3x-y-z=2的解,因此__________是方程组
这三对数值中,__________是方程x+2y+z=3的解,__________是方程2x-y-z=1的解,__________是方程3x-y-z=2的解,因此__________是方程组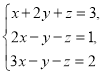 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
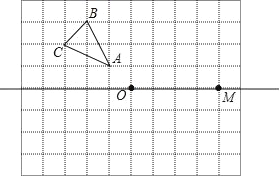
【题目】如图,它是一个8×10的网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
(1)画出△ABC关于直线OM对称的△A1B1C1.
(2)画出△ABC关于点O的中心对称图形△A2B2C2.
(3)△A1B1C1与△A2B2C2组成的图形是轴对称图形吗?如果是,请画出对称轴.△A1B1C1与△A2B2C2组成的图形 (填“是”或“不是”)轴对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,求∠A+∠AEC+∠C的度数.
解:过点E作EF∥AB.
∵EF∥AB(已作)
∴∠A+∠AEF=180°(______)
又∵AB∥CD(已知)
∴EF∥CD(______)
∴∠CEF+∠______=180°(两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C=360°(等式性质)
即∠A+∠AEC+∠C=______.
(2)根据上述解题及作辅助线的方法,在图2中,AB∥EF,则∠B+∠C+∠D+∠E=______.
(3)根据(1)和(2)的规律,图3中AB∥GF,猜想:∠B+∠C+∠D+∠E+∠F=______.
(4)如图4,AB∥CD,在B,D两点的同一侧有M1,M2,M3,…Mn共n个折点,则∠B+∠M1+∠M2+…+∠Mn+∠D的度数为______(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点.
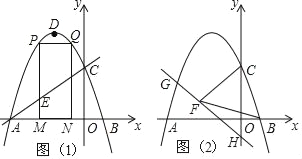
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
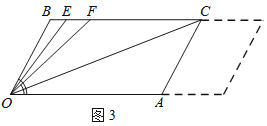
【题目】已知:BC∥OA,∠B=∠A=120°,试回答下列问题:
(1)如图1所示,求证:OB∥AC;

(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF,则∠EOC的度数是______;

(3)在(2)的条件下,若平行移动AC,其它条件不变,如图3,则∠OCB:∠OFB的值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10, ![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正确的序号是______.
∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正确的序号是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com