
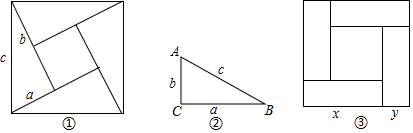
·ÖĪö £Ø1£©øł¾Ż“óÕż·½ŠĪµÄĆ껿µÄ²»Ķ¬±ķŹ¾·½·Ø£¬¼“æɵƵ½ÓŚa£¬b£¬cµÄµČŹ½£»
£Ø2£©øł¾Ż£Øa+b£©2=64£¬a2+b2=c2=36£¬¼“æɵƵ½ab=14£¬½ų¶ųµĆ³ö”÷ABCµÄĆ껿£»
£Ø3£©øł¾ŻĶźČ«Ę½·½¹«Ź½ŅŌ¼°Ę½·½²ī¹«Ź½£¬¼“æɵƵ½xy£¬x+y£¬x2-y2ŅŌ¼°x2+y2Ö®¼äµÄŹżĮæ¹ŲĻµ£¬½ų¶ųµĆ³öÕżČ·½įĀŪ£®
½ā“š ½ā£ŗ£Ø1£©“óÕż·½ŠĪµÄĆ껿=c2£¬
“óÕż·½ŠĪµÄĆ껿=4”Į$\frac{1}{2}$ab+£Øb-a£©2£¬
”ą4”Į$\frac{1}{2}$ab+£Øb-a£©2=c2£¬
”ą2ab+b2-2ab+a2=c2£¬
¼“a2+b2=c2
£Ø2£©”ßa+b=8£¬
”ą£Øa+b£©2=64£¬¼“a2+2ab+b2=64£¬
ÓÖ”ßa2+b2=c2=36£¬
”ą2ab=64-36=28£¬¼“ab=14£¬
”ą”÷ABCµÄĆ껿ĪŖ$\frac{1}{2}$ab=$\frac{1}{2}$”Į14=7
¹Ź“š°øĪŖ£ŗ7£»
£Ø3£©”ß¾ŲŠĪµÄ±ß³¤·Ö±šĪŖx£¬y£¬
”ą¾ŲŠĪµÄĆ껿=xy=£Øm2-n2£©”Ā4=$\frac{{m}^{2}-{n}^{2}}{4}$£»
”ß“óÕż·½ŠĪµÄ±ß³¤ĪŖm£¬
”ąx+y=m£»
”ߊ”Õż·½ŠĪµÄ±ß³¤ĪŖn£¬
”ąx-y=n£¬
”ąx2-y2=£Øx+y£©£Øx-y£©=m•n£»
”ßx+y=m£¬xy=$\frac{{m}^{2}-{n}^{2}}{4}$£¬
”ąx2+y2=£Øx+y£©2-2xy=m2-2”Į$\frac{{m}^{2}-{n}^{2}}{4}$=$\frac{{m}^{2}+{n}^{2}}{2}$£»
¹ŹĘäÖŠÕżČ·µÄÓŠ£Ø1£©£Ø2£©£Ø3£©£Ø4£©£®
¹Ź“š°øĪŖ£ŗ£Ø1£©£Ø2£©£Ø3£©£Ø4£©£®
µćĘĄ ±¾ĢāÖ÷ŅŖæ¼²éĮĖĶźČ«Ę½·½¹«Ź½µÄ¼øŗĪ±³¾°ŅŌ¼°¹“¹É¶ØĄķµÄÖ¤Ć÷£¬½āĢāŹ±×¢Ņā£ŗÖ¤Ć÷¹“¹É¶ØĄķŹ±£¬ÓĆ¼øøöČ«µČµÄÖ±½ĒČż½ĒŠĪĘ“³ÉŅ»øö¹ęŌņµÄĶ¼ŠĪ£¬Č»ŗóĄūÓĆ“óĶ¼ŠĪµÄĆ껿µČÓŚ¼øøöŠ”Ķ¼ŠĪµÄĆ껿ŗĶ£¬»Æ¼ņÕūĄķµĆµ½¹“¹É¶ØĄķ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -$\frac{1}{2}$ | B£® | -$\frac{\sqrt{2}}{2}$ | C£® | -$\frac{\sqrt{3}}{2}$ | D£® | -$\sqrt{3}$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
| ½ā£ŗx2-7x+10=0 a=1 b=-7 c=10 ”ßb2-4ac=9£¾0 ”ąx=$\frac{-b”Ą\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{7+3}{2}$ ”ąx1=5£¬x2=2 ĖłŅŌ£¬µ±ŃüĪŖ5£¬µ×ĪŖ2Ź±£¬µČŃüČż½ĒŠĪµÄČżĢõ±ßĪŖ5£¬5£¬2£® µ±ŃüĪŖ2£¬µ×ĪŖ5Ź±£¬µČŃüČż½ĒŠĪµÄČżĢõ±ßĪŖ2£¬2£¬5£® |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
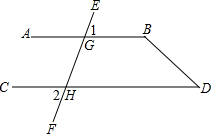 ČēĶ¼ŅŃÖŖ”Ļ1=”Ļ2£¬”ĻD=50”ć£¬
ČēĶ¼ŅŃÖŖ”Ļ1=”Ļ2£¬”ĻD=50”ć£¬²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
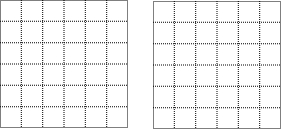 ČēĶ¼£¬Õż·½ŠĪĶųĀēÖŠµÄĆæøöŠ”Õż·½ŠĪ±ß³¤¶¼ĪŖ1£¬ĆæøöŠ”Õż·½ŠĪµÄ¶„µć½Šøńµć£¬·Ö±š°“ĻĀĮŠŅŖĒó»ŅŌøńµćĪŖ¶„µćČż½ĒŠĪŗĶĘ½ŠŠĖıߊĪ£®£ØĪŽŠčŠ“»·Ø£©
ČēĶ¼£¬Õż·½ŠĪĶųĀēÖŠµÄĆæøöŠ”Õż·½ŠĪ±ß³¤¶¼ĪŖ1£¬ĆæøöŠ”Õż·½ŠĪµÄ¶„µć½Šøńµć£¬·Ö±š°“ĻĀĮŠŅŖĒó»ŅŌøńµćĪŖ¶„µćČż½ĒŠĪŗĶĘ½ŠŠĖıߊĪ£®£ØĪŽŠčŠ“»·Ø£©²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
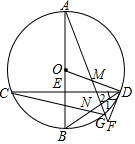 ČēĶ¼£¬ŌŚ”ŃOÖŠ£¬Ö±¾¶AB¾¹żĻŅCDµÄÖŠµćE£¬µćMŌŚODÉĻ£¬AMµÄŃÓ³¤Ļß½»”ŃOÓŚµćG£¬½»¹żDµÄÖ±ĻßÓŚF£¬”Ļ1=”Ļ2£¬Į¬½įBDÓėCG½»ÓŚµćN£®
ČēĶ¼£¬ŌŚ”ŃOÖŠ£¬Ö±¾¶AB¾¹żĻŅCDµÄÖŠµćE£¬µćMŌŚODÉĻ£¬AMµÄŃÓ³¤Ļß½»”ŃOÓŚµćG£¬½»¹żDµÄÖ±ĻßÓŚF£¬”Ļ1=”Ļ2£¬Į¬½įBDÓėCG½»ÓŚµćN£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com