
【题目】(1)如图,已知在△ABC中,∠BAC=40°,BD⊥AC于D,CE⊥AB于E,BD、CE所在直线交于点F,求∠BFC的度数;
(2)在(1)的基础上,若∠BAC每秒扩大10°,且在变化过程中∠ABC与∠ACB始终保持是锐角,经过t秒(0<t<14),在∠BFC,∠BAC这两个角中,当一个为另一个的两倍时,求t的值;
(3)在(2)的基础上,∠ABD与∠ACE的角平分线交于点G,∠BGC是否为定值,如果是,请直接写出∠BGC的值,如果不是,请写出∠BGC是如何变化的.

【答案】(1)140°;(2)t=2或8;(3)∠BGC是定值,为90°.
【解析】
(1)利用钝角的余角相等,证明∠CFD=∠A即可解决问题.
(2)由题意∠A=40°+10°×t,∠BFC=180°﹣∠A=140°﹣10°×t.分两种情形:①当0<t<5时,∠BFC=2∠A.②当5<t<14时,∠A=2∠BFC,分别构建方程求解即可.
(3)如图,结论∠BGC是定值.想办法证明∠G=∠A+∠ABG+∠ACG,∠ABG+∠ACG=∠ABD即可解决问题.
解:(1)∵BD⊥AC于D,CE⊥AB于E,
∴∠AEC=∠BDC=90°,
∴∠A+∠ACE=90°,∠ACE+∠CFD=90°,
∴∠CFD=∠A
∴∠BFC=180°﹣∠DFC=180°﹣∠A=140°.
(2)由题意∠A=40°+10°×t,∠BFC=180°﹣∠A=140°﹣10°×t.
①当0<t<5时,∠BFC=2∠A,则有140﹣10t=2(40+10t),
解得t=2.
②当5<t<14时,∠A=2∠BFC,
∴40+10t=2(140﹣10t),
解得t=8,
综上所述,当t=2或8时,∠BFC,∠A两个角中,一个角是另一个角的两倍.
(3)如图,结论∠BGC是定值.
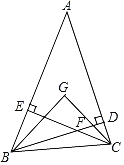
理由:∵BD⊥AC于D,CE⊥AB于E,
∴∠AEC=∠ADB=90°,
∴∠A+∠ABD=90°,∠A+∠ACE=90°,
∴∠ABD=∠ACE,
∵BG平分∠ABD,CG平分∠ACB,
∠ABG=![]() ∠ABD,∠ACG=
∠ABD,∠ACG=![]() ∠ACE,
∠ACE,
∴∠ABG+∠ACG=![]() (∠ABD+∠ACE)=∠ABD,
(∠ABD+∠ACE)=∠ABD,
∵∠A+∠ABG+∠GBC+∠GCB+∠ACG=180°,∠G+∠GBC+∠GCB=180°,
∴∠G=∠A+∠ABG+∠ACG=∠A+∠ABD=90°,
∴∠BGC是定值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴与
轴与![]() 轴上,且点
轴上,且点![]() ,点
,点![]() ,点
,点![]() 为矩形
为矩形![]() 、
、![]() 两边上的一个点.
两边上的一个点.

(1)当点![]() 与
与![]() 重合时,求直线
重合时,求直线![]() 的函数解析式;
的函数解析式;
(2)如图②,当![]() 在
在![]() 边上,将矩形沿着
边上,将矩形沿着![]() 折叠,点
折叠,点![]() 对应点
对应点![]() 恰落在
恰落在![]() 边上,求此时点
边上,求此时点![]() 的坐标.
的坐标.
(3)是否存![]() 在使
在使![]() 为等腰三角形?若存在,直接写出点
为等腰三角形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 480 | 601 | 1800 |
摸到白球的频率 |
|
|
|
|
|
|
|
(1)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为______.
(2)试估算盒子里黑、白两种颜色的球各有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E为AB边上一点,连接DE,将△ADE绕点D逆时针旋转90°得到△CDF,作点F关于CD的对称点,记为点G,连接DG.
(1)依题意在图1中补全图形;
(2)连接BD,EG,判断BD与EG的位置关系并在图2中加以证明;
(3)当点E为线段AB的中点时,直接写出∠EDG的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD和∠BDC的平分线相交于点E,BE交CD于点F,∠1+∠2=90°.试说明:(1)直线AB//CD.(2) 如果∠1=55°,求∠3的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于任何数a,符号[a]表示不大于a的最大整数.例如:[5.7]=5,[5]=5,[-1.5]=-2.
(1)[-π]= ;
(2)如果[a]=2,那么a的取值范围是 ;
(3)如果[![]() ]=-5,求满足条件的所有整数x;
]=-5,求满足条件的所有整数x;
(4)直接写出方程6x-3[x]+7=0的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下面证明过程补充完整
如图,已知AD⊥BC于D,点E在BA的延长线上,EG⊥BC于C,交AC于点F,∠E=∠1.求证:AD平分∠BAC.

证明:∵AD⊥BC于D,EG⊥BC于G( ),
∴∠ADC=∠EGC=90°( ),
∴AD∥EG( ),
∴∠1=∠2( ),
∴_____=∠3( ),
又∵∠E=∠1(已知),∴∠2=∠3( ),
∴AD平分∠BAC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(x,y),点B(x﹣my,mx﹣y)(其中m为常数,且m≠0),则称B是点A的“m族衍生点”.例如:点A(1,2)的“3族衍生点”B的坐标为(1﹣3×2,3×1﹣2),即B(﹣5,1).
(1)点(2,0)的“2族衍生点”的坐标为 ;
(2)若点A的“3族衍生点”B的坐标是(﹣1,5),则点A的坐标为 ;
(3)若点A(x,0)(其中x≠0),点A的“m族衍生点“为点B,且AB=OA,求m的值;
(4)若点A(x,y)的“m族衍生点”与“﹣m族衍生点”都关于y轴对称,则点A的位置在 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com