��2008•���ݣ�1�µף�ij��˾����11000ǧ�˗ո̿�棬��Щ�ո̵�����������60�죬60�����ėո̲��������ۣ���Ҫ������������������Ϊ0.05Ԫ/ǧ�ˣ������㣬�ո̵����ۼ۸�Ϊ2Ԫ/ǧ��ʱ��ƽ��ÿ����۳�100ǧ�ˣ����ۼ۸ͣ������������ӣ�ÿ����0.1Ԫ/ǧ�ˣ�ÿ��ɶ��۳�50ǧ�ˣ�
��1�������2Ԫ/ǧ�˵ļ۸����ۣ��ܷ���60����������Щ�ո̰��˼۸����ۣ���õ���ë�����Ƕ���Ԫ����ë����=����������-��洦���ѣ���
��2����ո����ۼ۸�Ϊx��0��x��2��Ԫ/ǧ��ʱ��ƽ��ÿ�����۳�yǧ�ˣ���y����x�ĺ�������ʽ�����Ҫ��2�·�������Щ�ո̣�2�·ݰ�28����㣩����ô���ۼ۸���߿ɶ�Ϊ����Ԫ/ǧ�ˣ���ȷ��0.1Ԫ/ǧ�ˣ���
���𰸡�
��������1��100×60=6000kg������11000kg��������60�������꣮������Ϊ6000×2-5000×0.05=11750Ԫ��
��2����������y����x�ĺ�������ʽ�ɵ�y=100+
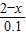
×50=-500x+1100����Ҫ��2�·�������Щ�ո̣��ۼ�x��������28��-500x+1100����11000���x��ȡֵ��Χ��
����⣺��1��100×60=6000��ǧ�ˣ���
�����60����������Щ�ո̣�
11000-6000=5000��ǧ�ˣ���
��60����п��5000ǧ�ˣ�
��ë����ΪW=6000×2-5000×0.05=11750Ԫ��
��2��y=100+
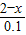
×50
=-500x+1100��0��x��2����
Ҫ��2�·�������Щ�ո̣��ۼ�x�������㲻��ʽ
28��-500x+1100����11000��
��x��
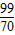
��1.414��
����Ҫ��2�·�������Щ�ո̣����ۼ���߿ɶ�Ϊ1.4Ԫ/ǧ�ˣ�
����������һ������һ�κ���������ʽģ�����������ĵ����⣮������Ҫע�⣺
�ڢ�С��ϼ���Ҫ�Ǽ������
�ڢ�С�⣬һЩѧ����������ʱû��ȥ���ǵ�ʣ�²��ֵĴ����ѣ����´�����һЩû�п�����Ӧ���Ӽ۸��´�����һЩ�����÷���ģ�������⣬���Ǻܺ�������Ӧ�������в���ʽ�����⣮
��Ŀ��������ѧ
��Դ��2008��ȫ���п���ѧ�����ࡶһ�κ�������04���������棩
���ͣ������
��2008•���ݣ�1�µף�ij��˾����11000ǧ�˗ո̿�棬��Щ�ո̵�����������60�죬60�����ėո̲��������ۣ���Ҫ������������������Ϊ0.05Ԫ/ǧ�ˣ������㣬�ո̵����ۼ۸�Ϊ2Ԫ/ǧ��ʱ��ƽ��ÿ����۳�100ǧ�ˣ����ۼ۸ͣ������������ӣ�ÿ����0.1Ԫ/ǧ�ˣ�ÿ��ɶ��۳�50ǧ�ˣ�
��1�������2Ԫ/ǧ�˵ļ۸����ۣ��ܷ���60����������Щ�ո̰��˼۸����ۣ���õ���ë�����Ƕ���Ԫ����ë����=����������-��洦���ѣ���
��2����ո����ۼ۸�Ϊx��0��x��2��Ԫ/ǧ��ʱ��ƽ��ÿ�����۳�yǧ�ˣ���y����x�ĺ�������ʽ�����Ҫ��2�·�������Щ�ո̣�2�·ݰ�28����㣩����ô���ۼ۸���߿ɶ�Ϊ����Ԫ/ǧ�ˣ���ȷ��0.1Ԫ/ǧ�ˣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ
��Դ��2008��ȫ���п���ѧ�����ࡶ����ʽ�벻��ʽ�顷��06���������棩
���ͣ������
��2008•���ݣ�1�µף�ij��˾����11000ǧ�˗ո̿�棬��Щ�ո̵�����������60�죬60�����ėո̲��������ۣ���Ҫ������������������Ϊ0.05Ԫ/ǧ�ˣ������㣬�ո̵����ۼ۸�Ϊ2Ԫ/ǧ��ʱ��ƽ��ÿ����۳�100ǧ�ˣ����ۼ۸ͣ������������ӣ�ÿ����0.1Ԫ/ǧ�ˣ�ÿ��ɶ��۳�50ǧ�ˣ�
��1�������2Ԫ/ǧ�˵ļ۸����ۣ��ܷ���60����������Щ�ո̰��˼۸����ۣ���õ���ë�����Ƕ���Ԫ����ë����=����������-��洦���ѣ���
��2����ո����ۼ۸�Ϊx��0��x��2��Ԫ/ǧ��ʱ��ƽ��ÿ�����۳�yǧ�ˣ���y����x�ĺ�������ʽ�����Ҫ��2�·�������Щ�ո̣�2�·ݰ�28����㣩����ô���ۼ۸���߿ɶ�Ϊ����Ԫ/ǧ�ˣ���ȷ��0.1Ԫ/ǧ�ˣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ
��Դ��2009�꽭��ʡ�γ�����������������һģ�Ծ������ʸ�������Ƽ���������棩
���ͣ������
��2008•���ݣ�1�µף�ij��˾����11000ǧ�˗ո̿�棬��Щ�ո̵�����������60�죬60�����ėո̲��������ۣ���Ҫ������������������Ϊ0.05Ԫ/ǧ�ˣ������㣬�ո̵����ۼ۸�Ϊ2Ԫ/ǧ��ʱ��ƽ��ÿ����۳�100ǧ�ˣ����ۼ۸ͣ������������ӣ�ÿ����0.1Ԫ/ǧ�ˣ�ÿ��ɶ��۳�50ǧ�ˣ�
��1�������2Ԫ/ǧ�˵ļ۸����ۣ��ܷ���60����������Щ�ո̰��˼۸����ۣ���õ���ë�����Ƕ���Ԫ����ë����=����������-��洦���ѣ���
��2����ո����ۼ۸�Ϊx��0��x��2��Ԫ/ǧ��ʱ��ƽ��ÿ�����۳�yǧ�ˣ���y����x�ĺ�������ʽ�����Ҫ��2�·�������Щ�ո̣�2�·ݰ�28����㣩����ô���ۼ۸���߿ɶ�Ϊ����Ԫ/ǧ�ˣ���ȷ��0.1Ԫ/ǧ�ˣ���
�鿴�𰸺ͽ���>>

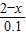 ×50=-500x+1100����Ҫ��2�·�������Щ�ո̣��ۼ�x��������28��-500x+1100����11000���x��ȡֵ��Χ��
×50=-500x+1100����Ҫ��2�·�������Щ�ո̣��ۼ�x��������28��-500x+1100����11000���x��ȡֵ��Χ��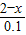 ×50
×50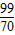 ��1.414��
��1.414��

 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�