
【题目】如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,![]() , C△ABC=10cm且∠C=60°.求:
, C△ABC=10cm且∠C=60°.求:
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)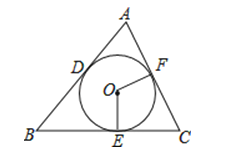
【答案】解:(1)连接OA,OB,OC,设⊙O的半径为r,
∵S△ABC=S△AOB+S△AOC+S△BOC ,
∴S△ABC=![]() ABr+
ABr+![]() BCr+
BCr+![]() ACr=
ACr=![]() (AB+BC+AC)r=
(AB+BC+AC)r=![]() C△ABCr,
C△ABCr,
∵![]() ,C△ABC=10cm,
,C△ABC=10cm,
∴r=2cm;
(2)∵∠C=60°,
∴∠EOF=120°,
∴S扇形OEF=![]() =
=![]() cm2;
cm2;
(3)∵∠C=60°,
∴∠EOF=120°,
∴C扇形OEF=l扇形OEF+2r=![]() +2×2=
+2×2=![]() +4(cm).
+4(cm).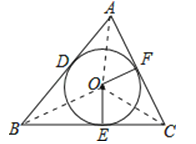
【解析】(1)连接OA,OB,OC,三角形ABC的面积等于△AOB、△AOC、△BOC的面积之和,从而得出圆的半径;
(2)根据∠C=60°,可得出∠EOF=120°,根据扇形的面积公式即可得出答案;
(3)由弧长公式求得弧EF的长,再加上半径的2倍即可.
【考点精析】根据题目的已知条件,利用三角形的内切圆与内心的相关知识可以得到问题的答案,需要掌握三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.


科目:初中数学 来源: 题型:
【题目】已知:在△ABC中, ∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
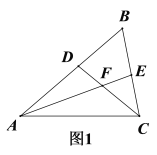
(1)如图1,若AE、CD为△ABC的角平分线. ①求证: ∠AFC=120°;②若AD=6,CE=4,求AC的长?
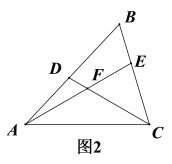
(2)如图2,若∠FAC=∠FCA=30°,求证:AD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
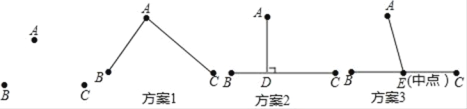
【题目】近年来,为减少空气污染,北京市一些农村地区实施了煤改气工程,某燃气公司要从燃气站点A向B,C两村铺设天然气管道,经测量得知燃气站点A到B村距离约3千米,到 C村距离约4千米,B,C两村间距离约5千米.下面是施工部门设计的三种铺设管道方案示意图.请你通过计算说明在不考虑其它因素的情况下,下面哪个方案所用管道最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=45°,点D是BC边上一动点(与点B,C不重合),点E与点D关于直线AC对称,连结AE,过点B作BF⊥ED的延长线于点F.
(1)依题意补全图形;
(2)当AE=BD时,用等式表示线段DE与BF之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并填空
问题:在一条直线上有A,B,C,D四个点,那么这条直线上总共有多少条线段?要解决这个问题,我们可以这样考虑,以A为端点的线段有AB,AC,AD 3条,同样以B为端点,以C为端点,以D为端点的线段也各有3条,这样共有4个3,即4×3=12(条),但AB和BA是同一条线段,即每一条线段重复一次,所以一共![]() 条线段. 那么,如果在一条直线上有5个点,则这条直线上共有_____________条线段. 如果在一条直线线上有n个点,那么这条直线上共有______________条线段.
条线段. 那么,如果在一条直线上有5个点,则这条直线上共有_____________条线段. 如果在一条直线线上有n个点,那么这条直线上共有______________条线段.
知识迁移:
如果在一个锐角∠AOB内部画2条射线OC,OD,那么这个图形中总共有____________个角,若在∠AOB内画n 条射线,则总共有___________个角.
学以致用:一段铁路上共有5个火车端,若一列客车往返过程中,必须停靠每个车站,则铁路局需为这段线路准备___________种不同的车票。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是8×8的正方形网格,每个小方格都是边长为1的正方形,A、B是格点(网格线的交点).以网格线所在直线为坐标轴,在网格中建立平面直角坐标系xOy,使点A坐标为(﹣2,4).
(1)在网格中,画出这个平面直角坐标系;
(2)在第二象限内的格点上找到一点C,使A、B、C三点组成以AB为底边的等腰三角形,且腰长是无理数,则点C的坐标是 ;并画出△ABC关于y轴对称的△A′B′C′.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB、AC边的垂直平分线分别交BC边于点M、N.
(1)如图①,若△AMN是等边三角形,则∠BAC= °;
(2)如图②,若∠BAC=135°,求证:BM2+CN2=MN2.
(3)如图③,∠ABC的平分线BP和AC边的垂直平分线相交于点P,过点P作PH垂直BA的延长线于点H.若AB=4,CB=10,求AH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=AC=2,点O是边BC的中点,半圆O与△ABC相切于点D、E,则阴影部分的面积等于( )
A.1﹣![]()
B.![]()
C.1﹣![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com