
����Ŀ����֪����ͼ����Rt��ACB�У���C=90����BC=3cm��AC=3![]() cm����P��B�������BA�������A�����˶����ٶ�Ϊ2cm/s����Q��A�������AC�������C�����˶����ٶ�Ϊ
cm����P��B�������BA�������A�����˶����ٶ�Ϊ2cm/s����Q��A�������AC�������C�����˶����ٶ�Ϊ![]() cm/s�������˶���ʱ��Ϊt(s)(0��t��3)������������⣺
cm/s�������˶���ʱ��Ϊt(s)(0��t��3)������������⣺
(1)��ͼ�٣�����PC����tΪ��ֵʱ��APC�ס�ACB����˵�����ɣ�
(2)��ͼ�ڣ�����P��Q�˶�ʱ���Ƿ����ijһʱ��t��ʹ�õ�P���߶�QC�Ĵ�ֱƽ�����ϣ���˵�����ɣ�
(3)��ͼ�ۣ�����P��Q�˶�ʱ���߶�BC���Ƿ����һ��G��ʹ���ı���PQGBΪ���Σ������ڣ������BG��������������˵�����ɣ�
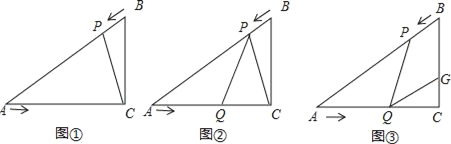
���𰸡�(1)t=![]() �����ɼ�������(2)���ڣ�t=1�����ɼ�������(3)�����ڣ����ɼ�����.
�����ɼ�������(2)���ڣ�t=1�����ɼ�������(3)�����ڣ����ɼ�����.
��������
��1�����ֱ�����������ʣ��ɡ�APC�ס�ACB����![]() ����2������P��PM��AC�������߶δ�ֱƽ�������ʣ���QM,AM�ı���ʽ��֤��APM�ס�ABC����
����2������P��PM��AC�������߶δ�ֱƽ�������ʣ���QM,AM�ı���ʽ��֤��APM�ס�ABC���� ![]() ��
�� ����3�������߶�BC���Ǵ���һ��G��ʹ���ı���PQGBΪƽ���ı��Σ���PQ��BG��PQ=BG���ɡ�APQ�ס�ABC����
����3�������߶�BC���Ǵ���һ��G��ʹ���ı���PQGBΪƽ���ı��Σ���PQ��BG��PQ=BG���ɡ�APQ�ס�ABC����![]() ��
��![]() ��BP=2t=3����PQ��BP.
��BP=2t=3����PQ��BP.
(1)��Rt��ACB����C=90����AC=3![]() cm��BC=3cm��
cm��BC=3cm��
��AB=6��
���˶�֪��BP=2t��AQ= ![]() ��
��
��AP=6��2t��
�ߡ�APC�ס�ACB��
![]()
��t= ![]() ��
��
(2)���ڣ�
���ɣ���ͼ�ڣ����˶�֪��BP=2t��AQ=![]() ��
��
��AP=6��2t��CQ= ![]() ��
��
�ߵ�P��CQ�Ĵ�ֱƽ�����ϣ�
����P��PM��AC��
��QM=CM= ![]()

��AM=AQ+QM= ![]() =
=![]() (3+t)
(3+t)
�ߡ�ACB=90������PM��BC��
���APM�ס�ABC
�� ![]()
����t=1��
(3)������
���ɣ����˶�֪��BP=2t��![]() ��
��
��AP=6��2t��
�����߶�BC���Ǵ���һ��G��ʹ���ı���PQGBΪƽ���ı��Σ�
��PQ��BG��PQ=BG��
���APQ�ס�ABC��![]() ��
��
��![]() ��
��
��BP=2t=3��
��PQ��BP��
��ƽ���ı���PQGB�����������Σ������߶�BC�ϲ�����һ��G��ʹ���ı���PQGBΪ���Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
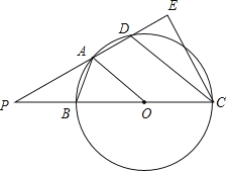
����Ŀ�� ��ͼ���ı���ABCD�ڽ�����BCΪֱ����Բ��Բ��ΪO����AB=AD���ӳ�CB��DA����P����C����PD�Ĵ��߽�PD���ӳ�����E����PB=BO������OA��
��1����֤��OA��CD��
��2�����߶�BC��DC��ֵ��
��3����CD=18����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����Ƕ���ֱ��y=ax-aΪ������y=ax2+bx+c��a��b��cΪ������a��0����������ֱ��������һ���������������ϣ�����һ��������y���ϵ�������Ϊ��������������������֪������![]() ����������ֱ��������A��B���㣨��A�ڵ�B����ࣩ����x�Ḻ���ύ�ڵ�C��
����������ֱ��������A��B���㣨��A�ڵ�B����ࣩ����x�Ḻ���ύ�ڵ�C��

��1����գ��������ߵ�������ֱ�����Ľ���ʽΪ ����A������Ϊ ����B������Ϊ ��
��2����ͼ����MΪ�߶�CB��һ���㣬����ACM��AM����ֱ��Ϊ�Գ��ᷭ�ۣ���C�ĶԳƵ�ΪN������AMNΪ�������ߵ��������������������N�����ꣻ
��3������E�������ߵĶԳ������˶�ʱ���ڸ������ߵ�������ֱ�����ϣ��Ƿ���ڵ�F��ʹ���Ե�A��C��E��FΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����E��F�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�ķ���![]() �Ľ�Ϊ�������Ҳ���ʽ��
�Ľ�Ϊ�������Ҳ���ʽ��![]() �⣬�������ķǸ�����a�У�������
�⣬�������ķǸ�����a�У�������
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ϣ�Сӱ��·��A�µ�B���������ߵ�C��ʱ�����Ӱ��CD�ij�Ϊ1�ף����������������ߵ�D��ʱ����ô�ʱӰ��DE��һ��E��·��A������Ϊ45������֪Сӱ������Ϊ1.5�ף���ô·��AB�ĸ߶��Ƕ����ף��� ��
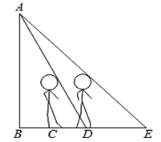
A.4��B.4.5��C.5��D.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ɳ��װ����5000m3ɳ�ӣ�����Ŀ�ĵغ�ʼжɳ����ƽ��жɳ�ٶ�Ϊv����λ��m3/Сʱ����жɳ�����ʱ��Ϊt����λ��Сʱ����
��1����v����t�ĺ�������ʽ�������б���㷨����������ͼ��
��2����Ҫ����20Сʱ��25Сʱ�ڣ���20Сʱ��25Сʱ��ж��ȫ��ɳ�ӣ���жɳ���ٶȷ�Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() ������������
������������![]() ������
������![]() ���ӳ�
���ӳ�![]() ����F����
����F����![]() Ϊ_______________
Ϊ_______________![]() ����
����![]() ����
����![]() ����Ϊ__________��
����Ϊ__________��
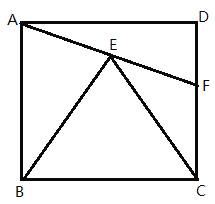
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ�����ͼ��ԭ�㼰�㣨![]() ��
�� ![]() ������ͼ����x�����һ���㵽ԭ��ľ���Ϊ1����ö��κ�������ʽ��
������ͼ����x�����һ���㵽ԭ��ľ���Ϊ1����ö��κ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��С�������������������˲���̤���ϣ���ס���֣�����·һ��̧�ȣ��ͻ����̤������������ת����ͼ2���Ӳ��濴��̤�徲ֹDE�ϵ��߶�AB�غϣ����BE��Ϊ0.21m����̤����������A��ת��AC��ʱ����á�CAB��42������C������ľ���CF��Ϊ0.52m����̤���������ŵ�A��ת��AG����GAB��30��ʱ�����G�������ĸ߶�GH�ij�������ȷ��0.1m���ο����ݣ�sin42���0.67��cos42���0.74��tan42���0.90��![]() ��
��
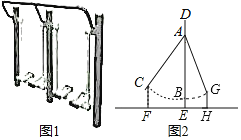
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com