
【题目】先阅读材料,然后按照要求答题。
阅读材料:为了解方程![]() ,我们可以将
,我们可以将![]() 视为一个整体,然后设
视为一个整体,然后设![]() ,
,![]() ,则原方程可化为:
,则原方程可化为:
![]() ①
①
解得:![]()
当![]() 时,
时,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴原方程的解为:![]() ,
,
解答问题:
(1)上述解题过程,在由原方程得到方程①的过程中,利用____________法达到了解方程的目的,体现了转化的数学思想;
(2)请利用以上知识解决问题:若![]() ,求
,求![]() 的值。
的值。
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
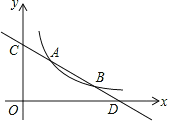
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲物体高4米,影长3米,乙物体高2米,影长4米,两物体相距5米.
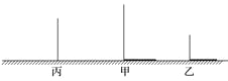
(1)在图中画出灯的位置,并画出丙物体的影子.
(2)若灯杆,甲、乙都与地面垂直并且在同一直线上,试求出灯的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仿照例题完成任务:
例:如图1,在网格中,小正方形的边长均为![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 都在格点上,
都在格点上,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
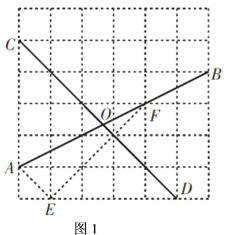
解析:连接![]() ,
,![]() ,导出
,导出![]() ,再根据勾股定理求得三角形各边长,然后利用三角函数解决问题.具体解法如下:
,再根据勾股定理求得三角形各边长,然后利用三角函数解决问题.具体解法如下:
连接![]() ,
,![]() ,则
,则![]() ,
,
![]() ,根据勾股定理可得:
,根据勾股定理可得:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 是直角三角形,
是直角三角形,![]() ,
,
![]()
即![]() .
.
任务:
(1)如图2,![]() ,
,![]() ,
,![]() ,
,![]() 四点均在边长为
四点均在边长为![]() 的正方形网格的格点上,线段
的正方形网格的格点上,线段![]() ,
,![]() 相交于点
相交于点![]() ,求图中
,求图中![]() 的正切值;
的正切值;
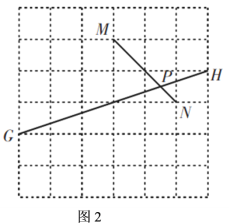
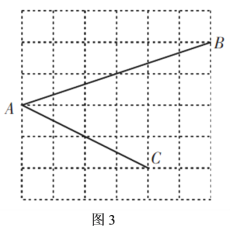
(2)如图3,![]() ,
,![]() ,
,![]() 均在边长为
均在边长为![]() 的正方形网格的格点上,请你直接写出
的正方形网格的格点上,请你直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=mx2﹣(2m+1)x+m﹣4的图象与x轴有两个公共点,m取满足条件的最小的整数
(1)求此二次函数的解析式
(2)当n≤x≤1时,函数值y的取值范围是﹣5≤y≤1﹣n,求n的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数![]() 的图象与两坐标轴所围成的图形最接近的面积是( )
的图象与两坐标轴所围成的图形最接近的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将背面完全相同,正面上分别写有数字1,2,3,4的四张卡片混合后,嘉辉从中随机地抽取一张,把卡片上的数字作为被减数。将形状、大小完全相同,分别标有数字1,2,3的三个小球混合后,向东从中随机地抽取一个,把小球上的数字作为减数,然后计算出这两数的差。
(1)请你用画树状图或列表的方法,求这两数的差为0的概率;
(2)嘉辉与向东做游戏,规则是:若这两数的差为非负数,则嘉辉赢;否则,向东赢。你认为该游戏公平吗?请说明理由。如果不公平,请你修改游戏规则,使游戏公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在研究如何在△ABC内做一个面积最大的正方形时,想到了可以利用位似知识解决这个问题,他的做法是:(如图1)先在△ABC内作一个小正方形DEFG,使得顶点D落在边AB上,顶点E、F落在边BC上,然后连接BG并延长交AC边于点H,作HK⊥BC,HI∥BC,再作IJ⊥BC于J,则正方形HIJK就是所作的面积最大的正方形.
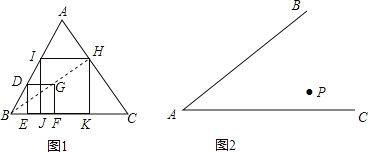
(1)若△ABC中,AB=4,∠ABC=60°,∠ACB=45°,请求出小明所作的面积最大的正方形的边长.
(2)拓展运用:
如图2,已知∠BAC,在角的内部有一点P,请画一个⊙M,使得⊙M经过点P,且与AB、AC都相切.(注:并简要说明画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2-2(m+1)x+2(m-1).
(1)求证:不论m取何值,抛物线必与x轴相交于两点;
(2)若抛物线与x轴的一个交点为(3,0),试求m的值及另一个交点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com