
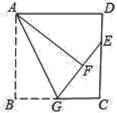
【题目】如图,正方形ABCD中,AB=6,G是BC的中点.将△ABG沿AG对折至△AFG,延长GF交DC于点E,则DE的长是___.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
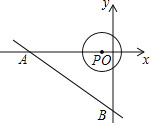
【题目】如图,直线y=-![]() x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
x-3交x轴于点A,交y轴于点B,点P是x轴上一动点,以点P为圆心,以1个单位长度为半径作⊙P,当⊙P与直线AB相切时,点P的坐标是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
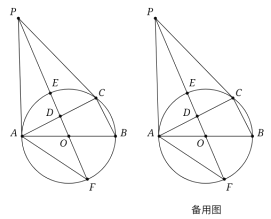
(1)证明:EF2=4ODOP;
(2)若tan∠AFP=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒 肺炎的防护知识,并鼓励社区居民在线参与作答《2020 年新型冠状病毒防治全国统一考试 (全国卷)》试卷(满分 100 分),社区管理员随机从甲、乙两个小区各抽取 20 名人员的 答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
乙小区:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据
60≤x≤70 | 70<x≤80 | 80<x≤90 | 90<x≤100 | |
甲小区 | 2 | 5 | 8 | 5 |
乙小区 | 3 | 7 | 5 | 5 |
分析数据
平均数 | 中位数 | 众数 | |
甲小区 | 85.75 | 87.5 | a |
乙小区 | 83.5 | b | 80 |
应用数据
(1)填空:a = ,b =___,
(2)若甲小区共有 800 人参与答卷,请估计甲小区成绩大于 90 分的人数为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,点K为弧AC上的一个动点(K不与A,C重合),AK,DC延长线交于点F,连接CK.
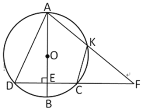
(1)求证:△ADF∽△CKF
(2)若AB=10,CD=6,求tan∠CKF的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆O的直径AB=12,点C是圆上一点,且∠ABC=30°,点P是弦BC上一动点,过点P作PD⊥OP交圆O于点D.

(1)如图1,当PD∥AB 时,求PD的长;
(2)如图2,当BP平分∠OPD时,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形![]() 中,点
中,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的两个动点(与点
上的两个动点(与点![]() 、
、![]() 、
、![]() 不重合),且始终保持
不重合),且始终保持![]() ,
,![]() ,
,![]() 交正方形外角平分线
交正方形外角平分线![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
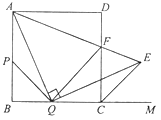
(1)求证:![]() ;
;
(2)证明:![]() ;
;
(3)设![]() ,当
,当![]() 为何值时,
为何值时,![]() ,并求出此时
,并求出此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】名闻遐迩的采花毛尖明前茶,成本每厅400元,某茶场今年春天试营销,每周的销售量y(斤)是销售单价x(元/斤)的一次函数,且满足如下关系:
x(元/斤) | 450 | 500 | 600 |
y(斤) | 350 | 300 | 200 |
(1)请根据表中的数据求出y与x之间的函数关系式;
(2)若销售每斤茶叶获利不能超过40%,该茶场每周获利不少于30000元,试确定销售单价x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
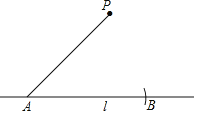
【题目】在数学课上,老师提出如下问题:如何使用尺规完成“过直线l外一点P作已知直线l的平行线”.
小明的作法如下:
①在直线l上取一点A,以点A为圆心,AP长为半径作弧,交直线l于点B;
②分别以P,B为圆心,以AP长为半径作弧,两弧相交于点Q(与点A不重合);
③作直线PQ.所以直线PQ就是所求作的直线.根据小明的作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB=AP= = .
∴四边形ABQP是菱形( )(填推理的依据).
∴PQ∥l.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com