
【题目】某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲乙两厂的印刷费用y(千元)与证书数量x(千个)的函数关系图象分别如图中甲、乙所示.

(1)填空:甲厂的制版费是________千元,当x≤2(千个)时乙厂证书印刷单价是________元/个;
(2)求出甲厂的印刷费y甲与证书数量x的函数关系式,并求出其证书印刷单价;
(3)当印制证书8千个时,应选择哪个印刷厂节省费用,节省费用多少元?
【答案】(1)1;1.5(2)y=0.5x+1(3)选择乙厂节省费用,节省费用500元
【解析】试题分析:(1)根据纵轴图象判断即可,用2到6千个时的费用除以证件个数计算即可得解;(2)设甲厂的印刷费y甲与证书数量x的函数关系式为y=kx+b,利用待定系数法解答即可;(3)用待定系数法求出乙厂x>2时的函数解析式,再求出x=8时的函数值,再求出甲厂印制1个的费用,然后求出8千个的费用,比较即可得解.
试题解析:(1)(1)由图可知,甲厂的制版费为1千元; 当x≤2(千个)时,乙厂证书印刷单价是3÷2=1.5元/个;
故答案为:1;1.5;
(2)解:设甲厂的印刷费y甲与证书数量x的函数关系式为y=kx+b, 可得: ![]() ,
,
解得: ![]() ,
,
所以甲厂的印刷费y甲与证书数量x的函数关系式为:y=0.5x+1
(3)解:设乙厂x>2时的函数解析式为y=k2x+b2 , 则 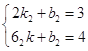 ,
,
解得 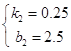 ,
,
∴y=0.25x+2.5,
x=8时,y=0.25×8+2.5=4.5千元,
甲厂印制1个证件的费用为:(4﹣1)÷6=0.5元,
印制8千个的费用为0.5×8+1=4+1=5千元,
5﹣4.5=0.5千元=500元,
所以,选择乙厂节省费用,节省费用500元.


科目:初中数学 来源: 题型:
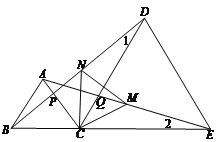
【题目】线段BE上有一点C,以BC,CE为边分别在BE的同侧作等边三角形ABC,DCE,连接AE,BD,分别交CD,CA于Q,P.
(1)找出图中的所有全等三角形.
(2)找出一组相等的线段,并说明理由.
(3)取AE的中点M、BD的中点N,连接MN,试判断三角形CMN的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表中的二次函数y=ax2+bx+c的自变量x与函数y的对应值,可判断二次函数的解析式为( )
x | … |
| 0 | 1 | 2 | … |
y | … |
|
|
|
| … |
A. y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() B. y=
B. y=![]() x2+
x2+![]() x﹣
x﹣![]()
C. y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() D. y=﹣
D. y=﹣![]() x2+
x2+![]() x+
x+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0)、B(2,0)两点,交y轴于点C(0,﹣2),过点A、C画直线.
(1)求二次函数的解析式;
(2)若点P在x轴正半轴上,且PA=PC,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
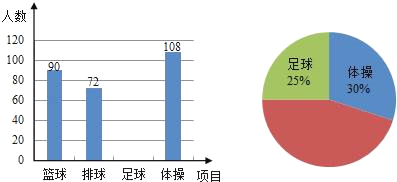
【题目】某中学进行体育教学改革,同时开设篮球、排球、足球、体操课、学生可根据自己的爱好任选其一,体育老师根据七年级学生的报名情况进行了统计,并绘制了下面尚未完整的条形统计图和扇形统计图.请根据统计图解答下列问题:
(1)该校七年级共有多少名学生?
(2)将两个统计图补充完整;
(3)从统计图中你还能得到哪些信息?(写出两条即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
试验种子n(粒) | 1 | 5 | 50 | 100 | 200 | 500 | 1000 | 2000 | 3000 |
发芽频数m | 1 | 4 | 45 | 92 | 188 | 476 | 951 | 1900 | 2850 |
发芽频率 | 0 | 0.80 | 0.90 | 0.92 | 0.94 | 0.952 | 0.951 | a | b |
(1)计算表中a,b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100kg麦种,则有多少千克的麦种可以成活为秧苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在《九章算术》中有求三角形面积公式“底乘高的一半”,但是在实际丈量土地面积时,量出高并非易事,所以古人想到了能否利用三角形的三条边长来求面积.我国南宋著名的数学家秦九韶(![]() 年—
年—![]() 年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元
年)提出了“三斜求积术”,阐述了利用三角形三边长求三角形面积方法,简称秦九韶公式.在海伦(公元![]() 年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前
年左右,生平不详)的著作《测地术》中也记录了利用三角形三边长求三角形面积的方法,相传这个公式最早是由古希腊数学家阿基米德(公元前![]() 年—公元前
年—公元前![]() 年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为
年)得出的,故我国称这个公式为海伦一秦九韶公式.它的表达为:三角形三边长分别为![]() 、
、![]() 、
、![]() ,则三角形的面积
,则三角形的面积![]() (公式里的
(公式里的![]() 为半周长即周长的一半).
为半周长即周长的一半).
请利用海伦一秦九韶公式解决以下问题:
(![]() )三边长分别为
)三边长分别为![]() 、
、![]() 、
、![]() 的三角形面积为__________.
的三角形面积为__________.
(![]() )四边形
)四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 的面积为__________.
的面积为__________.
(![]() )五边形
)五边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,五边形
,五边形![]() 的面积为__________.
的面积为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com