
【题目】如图1,⊙O是△ABC的外接圆,AP是⊙O的切线.已知AC=4,BC=5.

(1)求证:∠PAC=∠ABC;
(2)作∠BAC的平分线,与⊙O相交于点D,与BC相交于点E,连接并延长DC,与AP相交于点F(如图2),若AE=AC,求CF的长.
【答案】(1)见解析 (2)![]()
![]()
【解析】(1)作直径AQ,连接QC,根据切线的性质得出∠PAQ=90°,求出∠PAC+∠CAQ=90°,根据圆周角定理得出∠ACQ=90°,∠PAC=∠Q,即可求出答案;
(2)求出∠AEC=∠ACE,∠FAC=∠ABC,根据相似三角形的判定得出△FAC∽△ABC,得出比例式,代入求出即可.
(1)证明:
作直径AQ,连接QC,
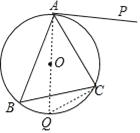
∵AP是⊙O的切线,
∴∠PAQ=90°,
∴∠PAC+∠CAQ=90°,
∵AQ是直径,
∴∠ACQ=90°,
∴∠CAQ+∠Q=90°,
∴∠PAC=∠Q,
∵∠Q=∠ABC,
∴∠PAC=∠ABC;
(2)解:∵AD是∠BAC的平分线,
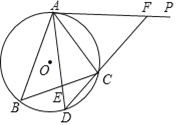
∴∠BAD=∠CAD,
∴∠ACF=∠ADC+∠CAD=∠ABC+∠BAD=∠AEC,
∵AE=AC,
∴∠AEC=∠ACE,
由(1)知:∠FAC=∠ABC,
∴△FAC∽△ABC,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴CF=![]() .
.


科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“武夷水秀”以特有的光影效果,吸引众多市民前去观看.特别是五一当天,共演了7场,平均每场有1200人观看,这天观看的总人数用科学记数法可以表示为( )
A.0.12×104
B.1.2×103
C.8.4×103
D.84×102
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校未为了解学生每天参加体育锻炼的时间情况,随机选取该校的部分学生进行调查.以下是根据调查结果绘制的统计图表的一部分.
组别 | A | B | C | D | E |
时间t/min | t<45 | 45≤t<60 | 60≤t<75 | 75≤t<90 | t≥90 |
人数 | 12 | 18 | m | 30 | 18 |
根据以上信息,解答下列问题:
(1)被调查的学生中,每天参加体育锻炼的时间不少于90min的有_____人,这些学生数占被调查总人数的百分比为_____%,每天参加体育锻炼的时间不足60min的有_____人;
(2)被调查的学生总数为_____人,统计表中m的值为_____,统计图中n的值为_____,被调查学生每天参加体育锻炼时间的中位数落在_____组;
(3)该校共有960名学生,根据调查结果,估计该校每天参加体育锻炼的时间不少于60min的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D,CD=3,则BC的长为( ) 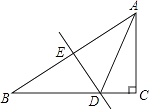
A.6
B.6 ![]()
C.9
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
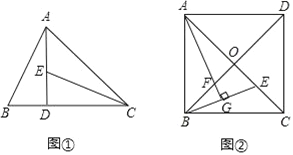
【题目】【阅读发现】如图①,在△ABC中,∠ACB=45°,AD⊥BC于点D,E为AD上一点,且DE=BD,可知AB=CE.
【类比探究】如图②,在正方形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交BD于点F.判断AF与BE的数量关系,并加以证明.
【推广应用】在图②中,若AB=4,BF=![]() ,则△AGE的面积为 .
,则△AGE的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com