
阅读材料:把形如ax2+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫做配方法.配方法的基本形式是完全平方公式的逆写,即a2±2ab+b2=(a±b)2.
例如:x2﹣2x+4=x2﹣2x+1+3=(x﹣1)2+ 3 ;
x2﹣2x+4=x2﹣4x+4+2x=(x﹣2)2+ 2x ;
x2﹣2x+4=![]() x2﹣2x+4+
x2﹣2x+4+![]() x2=(
x2=(![]() x﹣2)2+
x﹣2)2+ ![]() 是x2﹣2x+4的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项﹣﹣见横线上的部分).
是x2﹣2x+4的三种不同形式的配方(即“余项”分别是常数项、一次项、二次项﹣﹣见横线上的部分).
请根据阅读材料解决下列问题:
(1)比照上面的例子,将二次三项式x2﹣4x+9配成完全平方式(直接写出两种形式);
(2)将a2+3ab+b2配方(写两种形式即可,需写配方过程);
(3)已知a2+b2+c2﹣2ab+2c+1=0,求a﹣b+c的值.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:阅读理解
| 1 |
| 8 |
| 1 |
| 8 |
| M |
| N |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 8 |
| 1 |
| 8 |
| M |
| N |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 8 |
| 1 |
| 8 |
| M |
| N |
查看答案和解析>>
科目:初中数学 来源:泰州 题型:解答题
| 1 |
| 8 |
| 1 |
| 8 |
| M |
| N |
查看答案和解析>>
科目:初中数学 来源:2004年广东省深圳市实验中学高一直升考试数学试卷 (解析版) 题型:解答题
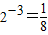 ,所以
,所以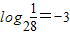 .
.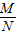 =______(a>0,a≠1,M、N均为正数).
=______(a>0,a≠1,M、N均为正数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com