练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．若方程3x2+bx+c=0的解为x1=1，x2=-3，则整式3x2+bx+c可分解因式为3（x-1）（x+3）．

    分析 根据因式分解解方程的方法得到原方程为3（x-1）（x+3）=0，于是3x2+bx+c分解为3（x-1）（x+3）．

    解答 解：∵方程3x2+bx+c=0的解为x1=1，x2=-3，
    ∴3（x-1）（x+3）=0，
    ∴3x2+bx+c可分解因式为3（x-1）（x+3）．
    故答案为3（x-1）（x+3）．

    点评 本题考查了解一元二次方程-因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．甲、乙两人共同解方程组$\left\{\begin{array}{l}{ax+5y=15①}\\{4x-by=-2②}\end{array}\right.$，由于甲看错了方程①中的a，得到方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$；乙看错了方程②中的b，得到方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$．试计算a2011+（-$\frac{1}{10}$b）2012=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．如图所示，直线AB，CD相交于O，若∠1=$\frac{2}{7}$∠2，则∠2=140度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

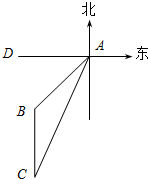    14．2014年3月8日凌晨2点40分，马来西亚航空公司的一架载有239人的波音777-200飞机与管制中心失去联系，我国救援船舰马上开展搜救工作，一艘搜救船与某日上午8点在A处望见西南方向有一座灯塔B（如图），此时测得船和灯塔相距60$\sqrt{2}$海里，船以每小时30海里的速度向南偏西24°的方向航行到C处，这时望见灯塔在船的正北方向（参考数据：sin24°≈0.4，cos24°≈0.9）．
    （1）求几点钟船到达C处；
    （2）求船到达C处时与灯塔之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，E、F是平行四边形ABCD的对角线AC上的点，AF=CE．
    （1）求证：四边形BFDE是平行四边形；
    （2）若AC=18，BE⊥AC于E，AB=9，BE=7，求AB与CD之间的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．关于x的一元二次方程（m-2）x2+3x+m2-4=0有一个根是0，则m的值为（　　）
    A．m=2B．m=-2C．m=-2或2D．m≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（-2，1），B（-1，4），C（-3，3）．
    （1）画出△ABC关于y轴对称的△A1B1C1，并写出A1点的坐标及sin∠B1A1C1的值；
    （2）以原点O为位似中心，位似比为1：2，在y轴的左侧，画出 将△ABC放大后的△A2B2C2，并写出A2点的坐标；
    （3）若点D（a，b）在线段AB上，直接写出经过（2）的变化后点D的对应点D2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

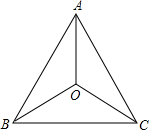    15．如图，O是正△ABC三条角平分线的交点．则下列说法错误的是（　　）
    A．△AOC与△BOC关于直线OC对称
    B．△AOC绕O点逆时针旋转240°与△COB重合
    C．△AOC绕O点顺时针旋转120°与△COB重合
    D．△AOC只通过平移就能与△BOC重合

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．将两张矩形纸片如图摆放，其中一矩形顶点落在另一矩形的边上，则∠1+∠2等于90°．

    查看答案和解析>>

    同步练习册答案