
科目:初中数学 来源: 题型:解答题
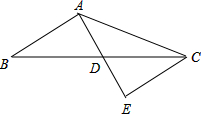 如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,延长AD到点E,使DE=AD,连接CE.
如图,在△ABC中,AB=6,AC=10,AD是BC边上的中线,且AD=4,延长AD到点E,使DE=AD,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
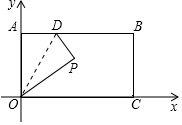 如图,长方形OABC的边OC、OA分别在x轴、y轴上,点B的坐标为($\sqrt{3}$,1)点D是AB边上一个动点(与点A不重合),沿OD将△OAD对折后,点A落到点P处,并满足△PCB是等腰三角形,则P点坐标为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)或($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).
如图,长方形OABC的边OC、OA分别在x轴、y轴上,点B的坐标为($\sqrt{3}$,1)点D是AB边上一个动点(与点A不重合),沿OD将△OAD对折后,点A落到点P处,并满足△PCB是等腰三角形,则P点坐标为($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)或($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
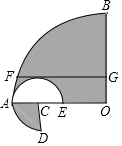 如图,扇形AOB与扇形DCE的圆心角分别为90°和270°,扇形DCE的弧过点A,FG∥AO,且与扇形DCE的弧相切,点F,G分别在弧AB,半径OB上,FG=2cm,则图中阴影部分的面积为πcm2.
如图,扇形AOB与扇形DCE的圆心角分别为90°和270°,扇形DCE的弧过点A,FG∥AO,且与扇形DCE的弧相切,点F,G分别在弧AB,半径OB上,FG=2cm,则图中阴影部分的面积为πcm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y3<y1<y2 | B. | y3<y2<y1 | C. | y1<y2<y3 | D. | y1<y3<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
| A. | 抛物线的开口向下 | B. | 当x>-3时,y随x的增大而增大 | ||
| C. | 二次函数的最小值是-2 | D. | 抛物线的对称轴x=-$\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com