
如图1,抛物线y=nx2-11nx+24n (n<0) 与x轴交于B、C两点(点B在点C的左侧),抛物线上另有一点A在第一象限内,且∠BAC=90°.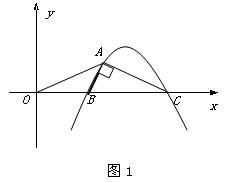
(1)填空:点B的坐标为(_ ),点C的坐标为(_ );
(2)连接OA,若△OAC为等腰三角形.
①求此时抛物线的解析式;
②如图2,将△OAC沿x轴翻折后得△ODC,点M为①中所求的抛物线上点A与点C两点之间一动点,且点M的横坐标为m,过动点M作垂直于x轴的直线l与CD交于点N,试探究:当m为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.
解:(1)B(3,0),C(8,0)
(2)①作AE⊥OC,垂足为点E
∵△OAC是等腰三角形,∴OE=EC=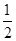 ×8=4,∴BE=4-3=1
×8=4,∴BE=4-3=1
又∵∠BAC=90°,∴△ACE∽△BAE,∴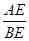 =
=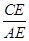
∴AE2=BE·CE=1×4,∴AE=2
∴点A的坐标为 (4,2)
把点A的坐标 (4,2)代入抛物线y=nx2-11nx+24n,得n=-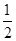
∴抛物线的解析式为y=-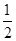 x2+
x2+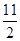 x-12
x-12
②∵点M的横坐标为m,且点M在①中的抛物线上
∴点M的坐标为 (m,-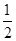 m2+
m2+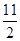 m-12),由①知,点D的坐标为(4,-2),
m-12),由①知,点D的坐标为(4,-2),
则C、D两点的坐标求直线CD的解析式为y=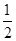 x-4
x-4
∴点N的坐标为 (m,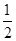 m-4)
m-4)
∴MN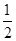 m2+
m2+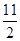 m-12)-(
m-12)-(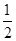 m-4)=-
m-4)=-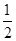 m2+5m-8
m2+5m-8
∴S四边形AMCN=S△AMN+S△CMN=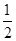 MN·CE=
MN·CE=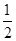 (-
(-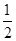 m2+5m-8)×4=-(m-5)2+9
m2+5m-8)×4=-(m-5)2+9
∴当m=5时,S四边形AMCN=9
解析


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
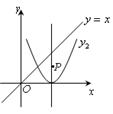
(1)如图,将抛物线y1=2x2向右平移2个单位,得到抛物线y2的图象,则y2= ;
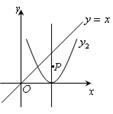
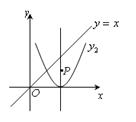
(2)P是抛物线y2对称轴上的一个动点,直线x=t平行于y轴,分别与直线y=x、抛物线y2交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·大连)(本题12分)如图15,抛物线y=ax2+bx+c经过A(-1,0)、B (3,
0)、C(0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于点M,连接PB.
(1)求该抛物线的解析式;
(2)抛物线上是否存在一点Q,使△QMB与△PMB的面积相等,若存在,求点Q的坐标;
若不存在,说明理由;
(3)在第一象限、对称轴右侧的抛物线上是否存在一点R,使△RPM与△RMB的面积相
等,若存在,直接写出点R的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年山东省九年级中考数学试卷4(解析版) 题型:解答题
如图1,抛物线y=nx2-11nx+24n (n<0) 与x轴交于B、C两点(点B在点C的左侧),抛物线上另有一点A在第一象限内,且∠BAC=90°.

(1)填空:点B的坐标为(_ ),点C的坐标为(_ );
(2)连接OA,若△OAC为等腰三角形.
①求此时抛物线的解析式;
②如图2,将△OAC沿x轴翻折后得△ODC,点M为①中所求的抛物线上点A与点C两点之间一动点,且点M的横坐标为m,过动点M作垂直于x轴的直线l与CD交于点N,试探究:当m为何值时,四边形AMCN的面积取得最大值,并求出这个最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com