
| A. | 平均数为2,众数为2,中位数为2 | B. | 平均数为3,众数为2,中位数为4 | ||
| C. | 平均数为2,众数为3,中位数为2 | D. | 平均数为2,众数为3,中位数为4 |
分析 针对选项C假设中位数为2,于是得到至少有四个数是小于等于2的,如果平均数为2,得到总和为20,因为前四个数都是小于等于2的非负数,故只可能为0,1,2,2;根据众数的意义得到3最少出现3次,于是得到必定存在的8个数使得这八个数的和3×3+2+0+0+1+1=13,分最大数为3时,最大数>3时,讨论即可.
解答 解:从中位数入手,假设中位数为2,
则至少有四个数是小于等于2的,
如果平均数为2,
则总和为20,
那么其中较小的9个数能满足和≥13的选项即可;
因为前四个数都是小于等于2的非负数,
故只可能为0,1,2;
那么其中必定有一个数出现两次,
又因为众数是3,所以3最少出现3次,
那么必定存在的8个数使得这八个数的和3×3+2+0+0+1+1=13,
当最大数为3时,显然符合题意;
当最大数>3时,又存在8个小于等于3的数的和为13,那么最大数必然不超过7;
故平均数为2,众数为3,中位数为2符合题意,
故选C.
点评 本题考查了众数,中位数,平均数的意义,熟记众数,中位数,平均数的意义是解题的关键.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:选择题
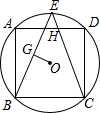 已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )
已知正方形ABCD内接于⊙O,⊙O的半径为3$\sqrt{2}$,点E是弧AD上的一点,连接BE,CE,CE交AD于H点,作OG垂直BE于G点,且OG=$\sqrt{2}$,则EH:CH=( )| A. | $\frac{1}{8}$ | B. | $\frac{2\sqrt{2}-1}{9}$ | C. | $\frac{2\sqrt{2}}{9}$ | D. | $\frac{\sqrt{2}}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
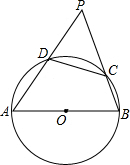 如图,AB是半圆O的直径,点C,D在半圆上,AD,BC的延长线相交于点P
如图,AB是半圆O的直径,点C,D在半圆上,AD,BC的延长线相交于点P查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
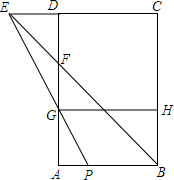 如图,矩形ABCD中,点F在AD上,AF=AB=12,点G是AF的中点,延长CD和BF交于点E,EG的延长线交AB于点P,GH∥AB交BC于点H,已知AP比ED小1.
如图,矩形ABCD中,点F在AD上,AF=AB=12,点G是AF的中点,延长CD和BF交于点E,EG的延长线交AB于点P,GH∥AB交BC于点H,已知AP比ED小1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com