
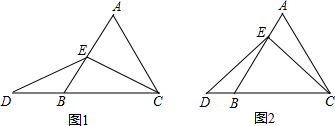
分析 (1)只要证明BD=BE即可解决问题.
(2)结论:AE=BD.如图2中,作EF∥BC交AC于F.只要证明△DBE≌△EFC,推出BD=EF=AE,推出BD=AE.
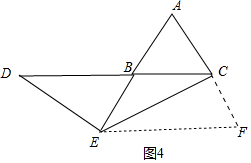
(3)分两种情形讨论如图3中,当E在BA的延长线上时,作EF∥AC交BD的延长线于F,易证△EBD≌△EFC,可得BD=CF=AE=2,CD=BD-BC=2-1=1.如图4中,当E在AB的延长线上时,作EF∥BC交AC的延长线于F,易证△EBD≌△CFE,可得BD=EF=AE=2,CD=BD+BC=2+1=3.由此即可解决问题.
解答 解:(1)如图1中,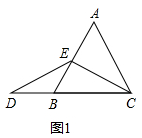
∵△ABC是等边三角形,AE=EB,
∴∠BCE=∠ACE=30°,∠ABC=60°,
∵ED=EC,
∴∠D=∠ECD=30°,
∵∠EBC=∠D+∠BED,
∴∠D=∠BED=30°,
∴BD=BE=AE.
(2)结论:AE=BD.理由如下:
如图2中,作EF∥BC交AC于F.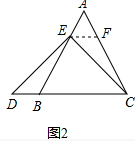
∵∠AEF=∠B=60°,∠A=60°,
∴△AEF是等边三角形,
∴AE=E=AFF,∠AFE=60°,
∴∠EFC=∠DBE=120°,
∵AB=AC,AE=AF,
∴BE=CF,
∵∠D=∠ECB=∠CEF,
在△DBE和△FEC中,
$\left\{\begin{array}{l}{∠DBE=∠EFC}\\{∠D=∠CEF}\\{BE=CF}\end{array}\right.$,
∴△DBE≌△EFC,
∴BD=EF=AE,
∴BD=AE,
(3)如图3中,当E在BA的延长线上时,作EF∥AC交BD的延长线于F,
易证△EBD≌△EFC,可得BD=CF=AE=2,CD=BD-BC=2-1=1.
如图4中,当E在AB的延长线上时,作EF∥BC交AC的延长线于F,
易证△EBD≌△CFE,可得BD=EF=AE=2,CD=BD+BC=2+1=3.
综上所述,CD的长为1或3.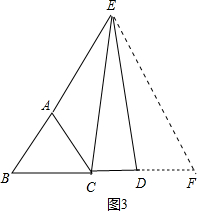
点评 本题考查三角形综合题、全等三角形的判定和性质、等边三角形的性质.等腰三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:解答题
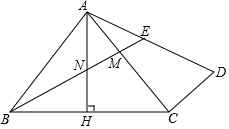 如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.
如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$是3的平方根 | B. | |$\sqrt{2}$-1|=$\sqrt{2}$-1 | ||
| C. | -$\sqrt{5}$的相反数是$\sqrt{5}$ | D. | 带根号的数都是无理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
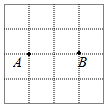 如图4×4的正方形网格每个小正方形的边长为1,每个小正方形的顶点叫格点,点A,B(均在格点上)的位置如图,若以A,B为顶点画面积为2的格点平行四边形,则符合条件的平行四边形的个数有( )
如图4×4的正方形网格每个小正方形的边长为1,每个小正方形的顶点叫格点,点A,B(均在格点上)的位置如图,若以A,B为顶点画面积为2的格点平行四边形,则符合条件的平行四边形的个数有( )| A. | 6 | B. | 7 | C. | 9 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com