
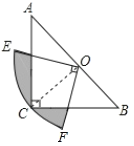
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
【答案】![]()
【解析】证明△AMO≌△CNO,将四边形CMON的面积转化为△ACO的面积,即可用割补法求出阴影部分的面积.
因为点O是AB的中点,所以AO=BO=CO,
由勾股定理得AB=![]() .
.
因为∠ACB=90°,∠EOF=90°,所以∠CMO+∠CNO=180°,又∠AMO+∠CMO=180°,所以∠AMO=∠CNO,
又因为∠A=∠B,AO=CO,
所以△AMO≌△CNO.
所以四边形CMON的面积=△CMO的面积+△CNO的面积
=△CMO的面积+△CNO的面积=△ACO的面积=△ABC面积的一半.
所以阴影部分的面积=扇形OEF的面积-四边形CMON的面积
=扇形OEF的面积-△ACO的面积
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,对角线
中,对角线![]() ,
,![]() 相交于
相交于![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,下列结论:①
的中点,下列结论:①![]() ;②四动形
;②四动形![]() 是平行四边形;③
是平行四边形;③![]() ;④
;④![]() 平分
平分![]() .其中正确的是( )
.其中正确的是( )
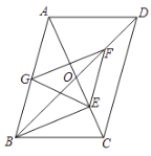
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
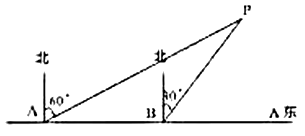
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,若点
,若点![]() 是
是![]() 的重心.则以下结论:①线段
的重心.则以下结论:①线段![]() ,
,![]() ,
,![]() 是
是![]() 的三条角平分线;②
的三条角平分线;②![]() 的面积是
的面积是![]() 面积的一半;③图中与
面积的一半;③图中与![]() 面积相等的三角形有5个;④
面积相等的三角形有5个;④![]() 的面积是
的面积是![]() 面积的
面积的![]() .其中一定正确的结论有( )
.其中一定正确的结论有( )
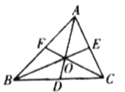
A.①②③B.②④C.③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买A、B两种型号电脑。已知每台A种型号电脑价格比每台B种型号电脑价格多0.1万元,且用10万元购买A种型号电脑的数量与用8万元购买B种型号电脑的数量相同.
(1)求A、B两种型号电脑每台价格各为多少万元?
(2)学校预计用不多于9.2万元的资金购进这两种电脑共20台,则最多可购买A种型号电脑多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com