
【题目】下列图形是将正三角形按一定规律排列,则第4个图形中所有正三角形的个数有( ) 
A.160
B.161
C.162
D.163
【答案】B
【解析】方法一: 解:第一个图形正三角形的个数为5,
第二个图形正三角形的个数为5×3+2=17,
第三个图形正三角形的个数为17×3+2=53,
第四个图形正三角形的个数为53×3+2=161,
故选B.
方法二:![]() ,
, ![]() ,
, ![]() ,
, 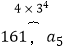 ,…
,… 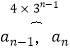 ,
,
∴  ,
,
(a2﹣a1)+(a3﹣a2)+(a4﹣a3)+…+(an﹣an﹣1)=an﹣a1 ,
∴an﹣a1=4×(3+32+…+3n﹣1)=4×(3+32+…+3n﹣1)= ![]() (用错位相减法可求出)
(用错位相减法可求出)
∴ ![]() ,
,
∵a1=5,
∴ ![]() .
.
由图可以看出:第一个图形中由角上的3个三角形加上中间1个小三角形再加上外围1个大三角形共有5个正三角形;下一个图形的三个角上的部分是上一个图形的全部,另外加上中间一个小的三角形和外围的一个大三角形,所以第二个图形中有5×3+1+1=17个正三角形,第三个图形中有17×3+1+1=53个正三角形,第四个图形中有53×3+1+1=161个正三角形.


科目:初中数学 来源: 题型:
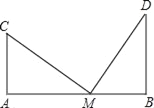
【题目】如图,两根旗杆AC与BD相距12m,某人从B点沿AB走向A,一定时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线夹角为90°,且CM=DM.已知旗杆AC的高为3m,该人的运动速度为0、5m/s,求这个人走了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:一列数x1,x2,x3,……,xn,从这列数的第二项数起,每一项与它前面的项的比都等于一个常数,就把这样的一列数叫做等比数列,这个常数叫做等比数列的公比.如1,2,4,8,…….这列数就是等比数列,公比是2.
(1)等比数列5,-15,45,-135,……,请计算这个等比数列的公比?
(2)若一个等比数列:-9,a,b,……,的公比是-![]() ,求a,b的值.
,求a,b的值.
(3)一个等比数列的第二项是-10,第三项是-20,求这组数列的第一项和第五项.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便居民低碳出行,聊城市公共自行车租赁系统(一期)试运行.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°. 
(1)求AD的长;
(2)求点E到AB的距离.(精确到0.1cm,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元问平均每人捐款是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到离家2400米的体育馆看球赛,进场时,发现门票还放在家中,此时离比赛还有40分钟,于是他立即步行(匀速)回家取票,在家取票用时2分钟,取到票后,他马上骑自行车(匀速)赶往体育馆.已知小明骑自行车从家赶往体育馆比从体育馆步行回家所用时间少20分钟,骑自行车的速度是步行速度的3倍.
(1)小明步行的速度(单位:米/分钟)是多少?
(2)小明能否在球赛开始前赶到体育馆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com