练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．计算：|-$\sqrt{2}$|-$\sqrt{8}$+（π-4）0．

    分析 原式利用绝对值的代数意义，二次根式性质，以及零指数幂法则计算即可得到结果．

    解答 解：原式=$\sqrt{2}$-2$\sqrt{2}$+1
    =1-$\sqrt{2}$．

    点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

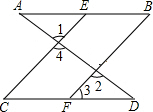    14．如图，已知AD与AB、CD交于A、D两点，EC、BF与AB、CD交于E、C、B、F，且∠1=∠2，∠B=∠C．
    （1）说明CE∥BF；
    （2）你能得出∠A=∠D这个结论吗？若能，写出你得出结论的过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

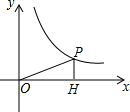    15．如图，P（12，a）在反比例函数$y=\frac{60}{x}$图象上，PH⊥x轴于H，则tan∠POH的值为$\frac{5}{12}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，在平面直角坐标系中，直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F，若点B的坐标为（m，2），则m的值可能为（　　）
    A．$\frac{1}{2}$B．$\frac{3}{2}$C．$\frac{5}{2}$D．$\frac{7}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

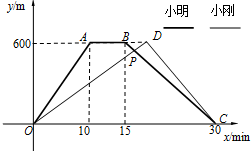    19．小明和小刚同时从公园门口出发，散步到公园“雨花亭”．他们离公园门口的距离y（m）与小刚行走的时间x（min）之间的关系如图．请根据图象回答：
    （1）小明到达“雨花亭”休息了5分钟；
    （2）求出图中BC段对应的函数表达式；
    （3）若小刚行走18分钟时两人相遇，求相遇点到公园门口的距离，并直接写出小刚从“雨花亭”回到公园门口所用的时间．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．下列运算中，正确的是（　　）
    A．x•x3=x3B．（x2）3=x5C．x6÷x2=x4D．（x-y）2=x2+y2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．（1）（2015-π）0+|$\sqrt{3}$-2|+$\sqrt{6}$$÷\sqrt{2}$+（$\frac{1}{3}$）-1；
    （2）先化简，再求值：（a-$\sqrt{3}$）（a+$\sqrt{3}$）-a（a-6），其中a=$\sqrt{5}$+$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列运算正确的是（　　）
    A．（2a2）3=6a6B．-x6÷x2=-x4C．2x+2y=4xyD．（x-1）2=x2-12

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

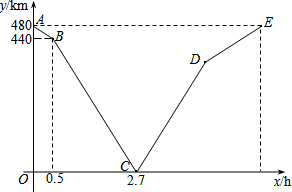    14．一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地．设先发车辆行驶的时间为xh，两车之间的距离为ykm，图中的折线表示y与x之间的函数关系．根据图象解决下列问题：
    （1）慢车的速度为80 km/h，快车的速度为120km/h；
    （2）求线段CD所表示的y与x之间的函数关系式，并写出自变量x的取值范围；
    （3）当x取何值时，两车之间的距离为300km？

    查看答案和解析>>

    同步练习册答案